Penyelesaian Pertidaksamaan Polinomial

Sobat Zenius, mungkin elo udah familiar dengan cara penyelesaian pertidaksamaan berikut: x – 4 > 2. Berapa, hasilnya? Yup, pasti elo bakal menjawab dengan x > 6. Jawaban elo betul, tapi, kali ini kita akan membahas pertidaksamaan polinomial dan cara kita mencari nilai x akan berbeda.

Gimana tuh, cara menyelesaikan pertidaksamaan polinomial? Simak artikel ini sampai akhir, ya!

Menentukan Nilai Titik Kritis

Dalam mencari nilai x pada sebuah pertidaksamaan polinomial, elo harus mencari yang namanya nilai titik kritis. Caranya adalah dengan menentukan letak nilai positif dan negatif dalam garis bilangan.

Sebagai contoh, gue akan pakai pertidaksamaan yang tadi, x – 4 > 2. Hasilnya tadi kan  x > 6 dan masih kita bisa ubah lagi menjadi  x – 6 > 0.  Kalau elo gambar garis bilangannya, jadinya akan seperti berikut:

Kenapa gue bisa tandai yang ke kiri negatif dan yang ke kanan positif? Kalau elo coba masukkan nilai x lebih kecil dari 6, elo akan mendapatkan hasil negatif. Tapi, kalau nilai x lebih besar dari 6, hasilnya akan positif.

Karena dalam pertidaksamaan, nilai x harus bisa menghasilkan x > 0, maka elo ambil nilai x yang hasilnya positif.

Jadi, nilai x yang memenuhi pertidaksamaan x – 6 > 0 adalah x > 6. Gampang, kan?

Nah, tapi, bentuk pertidaksamaan polinomial itu ada banyak sekali, dan penyelesaiannya juga beragam. Tapi tenang aja, gue udah siapkan beberapa contoh pertidaksamaan polinomial lengkap dengan penyelesaiannya supaya elo lebih mantap belajarnya. Yuk kita caw!

Baca Juga: Rumus Persamaan Kuadrat dan Akar-akarnya

Contoh Soal Pertidaksamaan Polinomial

1.

Untuk pertidaksamaan ini, kita gambar dulu garis-garis bilangannya.

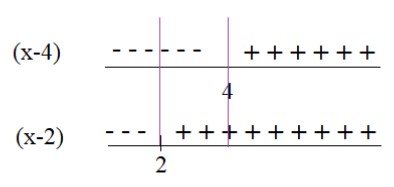
Setelah elo gambar, elo kalikan tanda- tanda positif dan negatif dari kedua garis bilangan di atas. Maka, elo akan mendapatkan garis bilangan seperti gambar berikut ini:

Jadi, nilai x yang memenuhi pertidaksamaan adalah atau

2.

Kalikan juga garis bilangannya seperti yang udah gue jelaskan tadi, dan elo akan mendapatkan garis bilangan berikut:

Jadi, nilai x yang memenuhi pertidaksamaan adalah atau .

3.

Supaya hasilnya lebih terjamin benernya, kita rapikan dulu yuk, pertidaksamaannya. Gue mau pindahin x yang ada di biar jadi di depan. Tapi kalau langsung ditukar aja tempatnya, jadinya malah , kan?

Biar lebih oke, kita hilangkan dulu tanda negatifnya dengan mengalikan pertidaksamaannya dengan -1 dan menjadi . Kalau sebuah pertidaksamaan dikalikan dengan -1, maka tandanya akan berubah jadi berlawanan arah.

Sekarang, kita buat garis bilangannya!

Jadi, nilai x yang memenuhi pertidaksamaan adalah atau .

Elo bisa nonton video penyelesaian pertidaksamaan polinomial ini lengkap dengan contoh lainnya, lho! Dimana? Tinggal klik aja banner berikut ini!

4.

Kali ini, kita punya bentuk kuadrat. Kalau elo hitung-hitung, mau berapapun nilai x nya kalau hasilnya dipangkatkan genap, pasti hasilnya positif, kan? Makanya elo nggak perlu repot-repot mengalikan garis bilangannya. Langsung aja pake yang .

Jadi, nilai x yang memenuhi pertidaksamaan di atas adalah .

5.

Kalau kita tinggalin aja yang berpangkat genap dan gambar garis bilangannya, maka akan menjadi seperti berikut:

Maka kita akan dapat nilai .

Tapi nih, meskipun yang berpangkat genap tadi kita cuekin karena nggak ada pengaruhnya ke garis bilangan, jangan dibiarkan begitu aja ya, nanti dia nangis. Mereka tetap bisa memenuhi pertidaksamaan dengan menghasilkan 0.

So, kita masih punya x = 2 dan x = -1.

Jadi, nilai x yang memenuhi pertidaksamaan tadi adalah x = -1 atau (ini udah termasuk x=2, yaps!)

6.

Sementara, kita punya nilai .

Coba elo cek lagi yang berpangkat genap. Ternyata, hasilnya 0. Yang diminta adalah nilai x yang memenuhi pertidaksamaan dan menghasilkan < 0. Berarti, x = -2, x = 1, dan x = 2 kita buang aja.

Maka, nilai x yang memenuhi pertidaksamaan adalah atau atau atau .

7.

Kalau pecahan gimana, dong? Caranya sama aja ya, elo gambar dulu garis bilangannya seperti biasa.

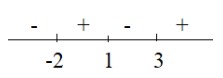
Maka elo bakal dapet atau . Tapi, perlu diingat, kalau dalam pecahan, apapun yang dibagi 0 hasilnya akan tidak terhingga. Jadi disini, penyebutnya harus .

Jadi, nilai x yang memenuhi pertidaksamaan adalah atau .

8.

Kok, nggak ada kurung-kurungnya? Tenang, ini masih kita bisa ubah bentuknya menjadi .

Jadi, nilai x yang memenuhi pertidaksamaan adalah atau . Jawaban ini juga bisa elo buktikan dengan menggambar grafiknya, lho! Caranya bisa elo simak di sini.

9.

Yang ini juga kita faktorkan dulu, ya. Hasilnya akan menjadi

Kalau elo gambar grafik pertidaksamaan tadi, elo akan punya kurva yang terbuka ke atas seperti berikut:

Maka, nilai x yang memenuhi adalah atau .

Baca Juga: Konsep, Grafik, & Rumus Fungsi Kuadrat

Penutup dan Contoh Soal Latihan

Ada berbagai bentuk dan cara penyelesaian pertidaksamaan polinomial dan elo baru aja mempelajarinya. Di penghujung artikel ini, gue mau kasih elo contoh-contoh soal lagi untuk elo coba kerjain sambil mengasah kemampuan elo.

1. Nilai x berikut ini yang memenuhi pertidaksamaan adalah ….
   A. 0
   B. 1
   C. 2
   D. 3
2. Penyelesaian dari pertidaksamaan adalah ….
   A.
   B. atau
   C.
   D. atau
3. Penyelesaian dari pertidaksamaan adalah ….
   A. atau
   B. atau
   C. atau
   D. atau

Pembahasan:

1. Jawaban: D. Garis bilangan pertidaksamaannya adalah sebagai berikut:

Maka, atau . Jadi, nilai x yang memenuhi yang ada dalam pilihan jawaban adalah 3.

2. Jawaban: D. Garis bilangan pertidaksamaannya adalah sebagai berikut:

Jadi, penyelesaiannya adalah atau

3. Jawaban: B. Garis bilangan pertidaksamaannya adalah sebagai berikut:

Jadi, penyelesaiannya adalah atau .

Oke deh, sekian dulu pembahasan pertidaksamaan polinomial di artikel ini. Jumpa lagi di tulisan gue lainnya, ya!

Baca Juga: Pengertian dan Penerapan Polinomial (Suku Banyak) – Materi Matematika Kelas 11