Halo Sobat Zenius! Pada artikel kali ini gue akan membahas materi fungsi Matematika kelas 10.

Mungkin dari elo ada yang bertanya-tanya sebenernya apa itu fungsi dalam Matematika?

Nah, kalau menurut KBBI (Kamus Besar Bahasa Indonesia), fungsi dalam Matematika adalah besaran yang berhubungan. Jika besaran yang satu berubah, besaran yang lain juga berubah.

Jadi intinya, ada relasi atau hubungan gitu di antara kedua fungsi tersebut.

Biar makin paham, coba elo liat contoh fungsi dalam Matematika berikut ini:

f(x)=2x+1

Kalo udah, pertanyaan selanjutnya adalah gimana cara memetakan nilai A ke B-nya kalau ada fungsi f(x) = 2x + 1?

Caranya elo buat dulu nilai A untuk disubstitusi dengan x. Kemudian, masukkan angkanya ke dalam fungsi f(x).

Misal: A = 1, dengan begitu:

B = 2 (x) + 1
B = 2(1) + 1 = 3, begitu seterusnya hingga seperti ini hasilnya:

fungsi matematika 2x+1 — *Fungsi matematika untuk f(x)=2x+1*

Elo pasti udah gak asing kan sama ilustrasi fungsi di atas? Nah, itulah yang disebut dengan fungsi matematika. Ini dia aturannya:

“Setiap anggota di A harus memiliki pasangan dengan tepat satu anggota di B”

Nah, dari ilustrasi di atas, elo bisa menuliskan nilai fungsi seperti berikut ini:

f(x): A → B

Keterangan:

A: domain (daerah asal)

B: kodomain (daerah kawan)

Sekarang elo udah tahu aturan dari fungsi, tapi ternyata fungsi ada banyak jenisnya lho.

Nah, supaya elo lebih paham, gue akan mengupas tuntas materi fungsi Matematika kelas 10 lengkap dengan contoh soal dan pembahasannya.

Tapi sebelum ini, elo harus belajar dulu cara membedakan antara fungsi dan bukan fungsi ya, langsung cek aja penjelasannya di bawah ini!

Daftar Isi

Gimana Cara Membedakan Antara Fungsi dan Bukan Fungsi?

Coba deh elo perhatikan ilustrasi berikut ini.

Untuk memperjelas aturan fungsi sebelumnya, elo langsung lihat ilustrasi di atas.

Pertanyaan: Manakah diagram yang termasuk fungsi dan manakah yang bukan fungsi?

Untuk menjawab, ingat ya aturan fungsi yang menyatakan bahwa “Setiap anggota di A harus memiliki pasangan dengan tepat satu anggota di B”. Dengan begitu, elo bisa nih menentukan bahwa:

(i) Bukan termasuk fungsi, karena ada anggota A yang gak memiliki pasangan di B.

(ii) Bukan termasuk fungsi, karena ada anggota A yang memiliki dua pasangan di B.

(iii) Termasuk fungsi, karena semua anggota A memiliki satu pasangan di B.

(iv) Termasuk fungsi, karena semua anggota A memiliki satu pasangan di B.

Lalu, bagaimana menentukan fungsi dan bukan fungsi dari suatu grafik?

Coba deh elo perhatikan gambar di bawah ini!

grafik fungsi dan bukan fungsi matematika zenius — grafik fungsi dan bukan fungsi matematika

Masih sama aturannya, bahwa setiap nilai A harus memiliki satu pasangan di B. Dengan begitu elo peroleh hasilnya:

(1) Termasuk fungsi, karena setiap x memiliki satu nilai y.

(2) Termasuk fungsi, karena setiap x memiliki satu nilai y, meskipun ada nilai x yang y-nya sama.

(3) Bukan termasuk fungsi, karena setiap nilai x memiliki dua nilai y.

(4) Bukan termasuk fungsi, karena setiap nilai x memiliki dua nilai y.

(5) Termasuk fungsi, karena setiap x memiliki satu nilai y.

(6) Termasuk fungsi, karena setiap nilai x memiliki satu nilai y.

Sampai sini jelas ya? Elo udah bisa membedakan manakah diagram dan grafik yang termasuk fungsi, sekaligus menjelaskan alasannya kenapa sih termasuk fungsi dan bukan fungsi.

Coba Latihan Soal: Membedakan Fungsi dan Bukan Fungsi

Domain Maksimum Fungsi Matematika

Elo udah tahu apa itu domain atau daerah asal, betul kan? Dari tadi elo berbicara mengenai domain yang berasal dari angka real seperti 2x+1. Nah, gimana kalau domainnya bukan angka real, melainkan dalam bentuk pecahan? Misalnya f(x) = $Pengertian dan Jenis Fungsi Matematika - Matematika Wajib Kelas 10 161$ .

Kalau x=0, berarti hasilnya akan menjadi tak terhingga. Intinya gak ada bilangan yang bisa dibagi dengan nol. Oleh karena itu, fungsi yang seperti ini domainnya harus didefinisikan. Elo perlu memperhatikan bahwa:

Bentuk fungsi pecahan () dapat terdefinisi jika x tidak sama dengan nol (x≠0) → D: {x | x ≠ 0, x ∈ R} atau D: {x | x < 0 v x > 0, x ∈ R}
Bentuk fungsi akar dapat terdefinisi jika x lebih dari atau sama dengan nol (x≥0), dan x bukan bilangan negatif.

Supaya lebih jelas, kita langsung masuk ke contohnya.

f(x) =

2x-8 ≥ 0

2x ≥ 8

x ≥ 4

Jadi, domain maksimum dari fungsi tersebut adalah x demikian hingga x lebih dari atau sama dengan 4 untuk x anggota himpunan bilangan real → D: {x | x ≥ 4, x ∈ R}.

Pelajari Selengkapnya: Materi Domain Maksimum Fungsi Resiprokal dan Akar

Jenis-Jenis Fungsi Matematika

Seperti yang gue janjikan tadi, materi fungsi matematika kelas 10 akan berlanjut dengan pengenalan jenis-jenis fungsi yang ada pada matematika.

Fungsi pertama yang akan elo pelajari adalah fungsi konstan atau polinom berderajat 0.

Fungsi Konstan (Polinom Berderajat 0)

Rumus fungsi matematika dari polinom berderajat 0 atau konstan adalah sebagai berikut:

f(x) = C, dengan c adalah nilai konstan

Contoh:

f(x) = 2 → artinya c bernilai 2, dengan setiap x anggota domain f, maka nilai f(x)=2.
f(x) = -1 → artinya c bernilai -1, dengan setiap x anggota domain f, maka nilai f(x)=-1.

Sekarang, kita coba cari tahu lagi, berapa sih himpunan berpasangan dari f(x)=2, dengan batas domain fungsinya yaitu Df: {x | -2 ≤ x ≤ 2}.

jenis fungsi konstanta zenius — Menentukan domain maksimum dan grafik dari jenis fungsi konstan

Contoh Soal Fungsi Konstan

Nah, supaya lebih paham tentang materi fungsi Matematika jenis konstan, elo bisa lihat contoh soal dan pembahasan di bawah ini ya:

f(x) = 2
f(x) = y = 2
maka x = 0
Coba gambarkan pada bidang kartesius…

Jawab:

Pengertian dan Jenis Fungsi Matematika - Matematika Wajib Kelas 10 165

Fungsi Linear (Polinom Berderajat 1)

Elo udah pernah belajar tentang persamaan linear kan? Nah, sekarang gue akan bahas jenis selanjutnya dalam materi fungsi kelas 10.

Namanya adalah fungsi linear, yaitu fungsi yang pangkat tertingginya sama dengan satu makanya nama lain dari fungsi ini adalah polinom berderajat 1.

Secara umum, rumus fungsi matematika jenis linear ini adalah sebagai berikut:

f(x) = ax + b, dengan a≠0

Contoh:

f(x) = x+3 → a=1, b=3

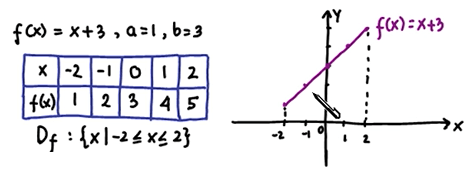
jenis fungsi linear zenius — contoh fungsi linear

Nah, dari contoh fungsi konstan dan linear di atas, elo bisa menyimpulkan bahwa grafik fungsi konstan ya akan selalu konstan atau sama (sejajar dengan sumbu-x). Sedangkan, grafik fungsi linear akan sama dengan grafik persamaan garis lurus.

Contoh Soal Fungsi Linear

Supaya makin paham, coba elo lihat contoh soal fungsi linear berikut ini:

Gambarlah grafik fungsi f(x) 2x + 1 dengan Df: {x | -1 ≤ x < 3, x ∈ bilangan bulat}.

Caranya gampang, elo tinggal buat tabel seperti di bawah ini untuk menentukan titik koordinatnya:

Pengertian dan Jenis Fungsi Matematika - Matematika Wajib Kelas 10 166

Nah, kalo udah ketemu titik-titiknya tinggal masukan ke dalam koordinat kartesius:

Pengertian dan Jenis Fungsi Matematika - Matematika Wajib Kelas 10 167

Pelajari Selengkapnya: Materi Fungsi Konstan dan Linear

Fungsi Polinomial

Fungsi polinomial sering juga disebut dengan suku banyak. Secara umum, bentuk umum dari fungsi polinomial, yaitu:

$Pengertian dan Jenis Fungsi Matematika - Matematika Wajib Kelas 10 168$

Bentuk fungsi polinom di atas disebut dengan fungsi polinom berderajat n.

Contoh:

f(x) = x^4 – 3x^2 + 1 → fungsi polinom berderajat 4.
f(x) = 1 – 2x + x^2 → fungsi polinom berderajat 2 (fungsi kuadrat).
f(x) = -5 → fungsi polinom berderajat 0 (fungsi konstan).
f(x) = 2x – 4 → fungsi polinom berderajat 1 (fungsi linear).

Contoh Fungsi Polinomial

Nah, supaya lebih memahami materi fungsi matematika kelas 10 jenis fungsi polinomial, coba lihat contoh soal fungsi polinom berderajat 2 atau fungsi kuadrat di bawah ini:

Grafik fungsi kuadrat y = x² -2x -24 memotong sumbu x di titik?

Jawab:

Ingat, syarat memotong sumbu x maka y = 0
x² -2x -24 = 0 (kemudian difaktorkan)
(x-6) (x+4)
Maka: x-6 = 0 dan x+4 = 0
x₁ = 6 dan x₂= -4
Titiknya adalah (6,0) dan (-4,0)

Pelajari Selengkapnya: Materi Fungsi Polinomial (Suku Banyak)

Fungsi Rasional

Sama seperti namanya, fungsi rasional menggunakan bilangan rasional, jadi rumus fungsi Matematika bilangan rasional adalah: Bil. rasional = a/b → b ≠ 0

Bentuk umum dari fungsi rasional yaitu:

$Pengertian dan Jenis Fungsi Matematika - Matematika Wajib Kelas 10 169$ , di mana p(x) dan q(x) merupakan fungsi polinomial,

dan

q(x) ≠ 0

Contoh:

, dengan syarat x+2 ≠ 0.

Contoh Soal Fungsi Rasional

Nah, supaya lebih paham, elo bisa lihat contoh soal fungsi rasional di bawah ini deh:

Diketahui: fungsi

Pengertian dan Jenis Fungsi Matematika - Matematika Wajib Kelas 10 171

Ditanya:
1) Domain f(x)
2) range f(x)
3) sumbu asimtot vertikal
4) sumbu asimtot horizontal
5) gambarkan grafiknya

Jawab:

Perlu elo ingat bahwa ini adalah fungsi rasional, artinya penyebut dalam fungsi

tidak boleh sama dengan nol. Sehingga…

x ≠ 0
x – 6 ≠ 0
x ≠ 6
Maka, Df: {x | x ≠ 6, x ∈ R}.

Hal pertama yang harus elo lakukan adalah mengubah fungsi f(x) menjadi x =
Caranya sebagai berikut:

Pengertian dan Jenis Fungsi Matematika - Matematika Wajib Kelas 10 173

Sumbu asimtot vertikal bisa didapatkan dari domain f(x) yang sudah dicari tadi.

Yaitu x ≠ 6

Maka sumbu asimtotnya adalah x = 6

Sumbu asimtot horizontal bisa didapatkan dari range f (x) yang sudah dicari tadi,
Yaitu y ≠ 1

Maka sumbu asimtotnya adalah y = 1

Grafik

Pertama, elo gambar sumbu asimtotnya dulu, karena udah diketahui di atas tinggal masukin aja:

Pengertian dan Jenis Fungsi Matematika - Matematika Wajib Kelas 10 175

Kalo udah, sekarang cari titiknya dengan persamaan sebagai berikut:

Pengertian dan Jenis Fungsi Matematika - Matematika Wajib Kelas 10 176

Nah, sekarang elo udah tau titiknya tinggal masukin aja ke grafik fungsi seperti ini:

Pengertian dan Jenis Fungsi Matematika - Matematika Wajib Kelas 10 177

Kemudian tinggal tarik garis sesuai titik, nantinya garisnya akan mendekati titik asimtot, seperti ini:

Pengertian dan Jenis Fungsi Matematika - Matematika Wajib Kelas 10 178

Pelajari Selengkapnya: Materi Fungsi Rasional

Fungsi Logaritma dan Eksponen

Jenis fungsi selanjutnya adalah fungsi logaritma dan eksponen. Tapi tau gak sih elo kenapa fungsi logaritma dan eksponen disatukan?

Sekarang coba kita ingat-ingat lagi tentang eksponen, misalnya a^b=c akan menghasilkan logaritma . Kalau kita masukkan angkanya, maka 2^3=8 akan menghasilkan logaritma .

Lalu, fungsi eksponen itu yang gimana sih? Nah, rumus fungsi Matematika dari eksponen adalah sebagai berikut:

f(x) = a^x, a>0, a≠1

Contoh:

f(x) = 3^x
f(x) = 5^x

Kemudian, bentuk rumus fungsi Matematika logaritma yaitu::

f(x) = , a>0, a≠1, x>0

Contoh:

f(x) = 2logx
f(x) = 3log(x+1)

Gimana caranya elo tahu antara fungsi eksponen dan logaritma saling berhubungan? Elo bisa lihat dari grafiknya. Perhatikan perhitungan di bawah ini!

fungsi logaritma dan eksponen zenius — *Hubungan antara fungsi logaritma dan fungsi eksponen*

Dari grafik antara fungsi logaritma dan eksponen, kalau elo beri garis potong di antara keduanya, maka akan menghasilkan pencerminan. Maka, hubungannya yaitu fungsi logaritma merupakan invers dari fungsi eksponen.

Contoh Fungsi Logaritma dan Eksponen

Nah, supaya lebih paham coba cek contoh soal fungsi logaritma berikut ini:

Carilah asal fungsi f(x) = log(4 – x²) adalah

Jawab:

Sebelum menjawab, ingat bahwa syarat pada logaritma akan mengubah

(4 – x²) > 0
x² – 4 < 0
(x-2) (x+2) < 0
Berarti daerah asal adalah {x | -2 < x < 2}.

Pelajari Selengkapnya: Materi Fungsi Logaritma dan Eksponensial

Oke, sampai sini gue harap elo udah lumayan paham ya mengenai pengertian fungsi Matematika beserta contohnya.

FYI nih, kalau elo termasuk orang yang lebih suka belajar menggunakan video, elo bisa mengakses video materi belajar tentang Domain Maksimum Fungsi Fungsi Resiprokal dan Akar hingga Jenis-jenis Fungsi dengan klik banner di bawah ini! Selamat belajar!

Pelajari materi Matematika di video materi belajar Zenius

Buat pengalaman belajar yang lebih seru, cobain akses lewat aplikasi Zenius secara GRATIS menggunakan akun yang sudah elo daftarkan sebelumnya. Elo juga bisa pilih berbagai paket belajar yang udah Zenius sesuaikan sama kebutuhan lo! Klik banner di bawah ini untuk info lengkapnya!