jenis matriks

Materi Matriks Matematika, Pengertian & Contoh Soal

Maulia Indriana Ghani

Jun 17, 2022 — 8 min read

matriks matematika (Arsip Zenius)

Sobat Zenius, elo pasti tau kan tentang materi matriks matematika? Mayoritas dari kita kalau mendengar kata Matematika bawaannya langsung malas dan pusing. Rasanya pengen banget deh menghindari pelajaran yang satu ini. Tapi, emang bisa ya? Tidak semudah itu Ferguso!

Matematika merupakan bahasa simbol yang bersifat universal. Hubungan antara matematika dan kehidupan kita itu sangat erat, sulit untuk dipisahkan. Banyak masalah dalam kehidupan sehari-hari kita yang diselesaikan dengan model matematika.

Contohnya apa aja? Pembuatan jurnal dan rapor yang mengandung banyak variabel, perhitungan populasi penduduk, rotasi dalam beberapa dimensi, kriptografi, persamaan reaksi, dan berbagai bidang IT.

Nah, semua contoh yang disebutkan barusan itu bisa menggunakan konsep aljabar linier, yaitu matriks. Yuk lanjut baca untuk lebih tau tentang materi matriks lengkap!

Apa Itu Matriks?

Sebelum masuk ke penjelasan apa itu matriks, gue mau elo coba perhatikan gambar di bawah ini dulu!

Udah pernah melihat model matematika seperti itu belum? Nah, itu yang disebut dengan matriks. Kalau kita simpulkan, matriks adalah susunan persegi/persegi panjang dari angka yang diatur dalam baris dan kolom.

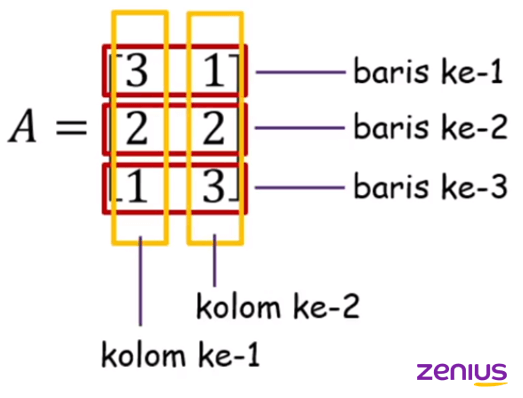
Susunan angka tersebut biasanya ditulis dalam kurung kotak. Dari model matematika di atas, kita bisa tau kalau matriks A punya 3 baris dan 2 kolom.

Lah, baris dan kolom itu yang gimana sih? Oke, kita bahas satu per satu ya. Elo bisa lihat pengertiannya di bawah ini.

Baris: susunan horizontal (kanan-kiri)
Kolom: susunan vertikal (atas-bawah)

Selain itu, ada juga yang namanya ordo. Suatu matriks dengan m baris dan n kolom disebut dengan matriks berordo mxn.

Dari gambar di atas, elo dapat menyebut bahwa A merupakan matriks dengan ordo 3×2.Ada juga yang namanya elemen atau unsur. Kita biasa mengenalnya ai,j, di mana i adalah baris dan j adalah kolom.

Misalnya, ada yang nanya gini, berapa elemen matriks a2,1? Berarti elo bisa cari di baris ke-2, kolom ke-1. Ketemu kan nilainya, yaitu 2. Supaya lebih jelas, elo bisa lihat uraian berikut ini.

a_1,1 → 3

a_2,1→ 2

a_3,1 → 1

a_1,2 → 1

a_2,2 → 2

a_3,2 → 3

Supaya makin paham, coba elo perhatikan matriks matematika di bawah ini:

Lalu, elo jawab pertanyaan di bawah ini:

Matriks di atas berordo berapa?
Tentukan nilai elemennya:
a_2,2= ….
a_1,3= ….
a_2,1= ….

Elo jawab di kolom komentar yaa! Oke, udah jelas ya sampai sini? Elo udah punya bekal nih, udah tau materi matriks itu apa, baris dan kolom yang seperti apa, dan udah bisa nentuin ukuran sekaligus elemen dari suatu matriks. Kalau gitu kita lanjut kenalan sama jenis-jenisnya ya.

Asyik banget nih kayaknya belajar materi matriks matematika. Udah pada download aplikasi Zenius belum nih? Download dulu yuk kalau belum. Nikmati akses fitur-fitur menarik yang cuma ada di aplikasi Zenius. Klik banner di bawah untuk langsung download ya!

Download Aplikasi Zenius

Tingkatin hasil belajar lewat kumpulan video materi dan ribuan contoh soal di Zenius. Maksimaln persiapanmu sekarang juga!

Sejarah Matriks Matematika

Sebelum masuk ke jenis-jenisnya, ada baiknya sih kita kenalan dulu sama asal mula materi matriks matematika. Elo tau gak kalau pada awal ilmu ini ada, namanya bukan matriks, melainkan suatu angka yang disusun secara persegi, disebut dengan determinan.

Seiring berjalannya waktu, ide matriks ini dikenal sebagai aljabar linier dan mulai banyak diaplikasikan pada berbagai cabang ilmu.

Dilansir dari Ensiklopedia Britannica, istilah matriks diperkenalkan oleh ahli matematika dari Inggris yang bernama James Joseph Sylvester (1814-1897) pada abad ke-19 atau sekitar tahun 1850-an.

Kemudian, seorang temannya bernama Arthur Cayley (1821-1895) yang pertama kali menerbitkan definisi abstrak matriks dalam “A Memoir on the Theory of Matrices” tahun 1858.

Cayley juga menerapkannya pada sistem persamaan linier dan menyatakan kalau ilmu yang satu ini cukup penting, misalnya membentuk sistem aljabar pada berbagai hukum aritmatika dan diaplikasikan dalam grafik komputer (rotasi, transformasi gambar, dll).

Jenis jenis Matriks

Jenis matriks matematika gak cuma satu Sobat Zenius, ada yang cuma sebaris, bentuk persegi, semua nilai elemennya nol, ada yang diagonalnya 1 dan lainnya nol, bahkan ada yang dibolak-balik. Penasaran? Langsung aja kita ulik, yuk!

Matriks Baris dan Kolom

Jenis yang satu ini terdiri dari satu baris (a1xn) atau kolom aja (anx1).

Matriks Baris

Matriks Kolom

Matriks Persegi

Jenis yang satu ini memiliki jumlah baris dan kolom sama, sehingga ordonya nxn.

Matriks Diagonal

Matriks yang elemen-elemen selain diagonal utamanya bernilai nol. Dari gambar di bawah ini, diagonal utama ditandai dengan warna merah. Bisa elo lihat juga di situ kalau semua yang ada di luar diagonal utama nilainya nol.

Matriks Skalar

Matriks diagonal yang semua elemen diagonal utamanya bernilai sama. Hampir mirip dengan matriks diagonal, perbedaannya terletak pada bilangan di diagonal utamanya. Kalau matriks diagonal itu bilangan penyusunnya beda-beda. Sedangkan pada matriks skalar, diagonal utamanya tersusun atas bilangan-bilangan yang sama. Seperti ini contohnya:

Matriks Identitas

Elo tau kan kalau semua bilangan yang dikalikan satu hasilnya adalah bilangan itu sendiri? Nah, bilangan satu di sini didefinisikan dengan matriks identitas.

[A] [I] = [I] [A] = [A]

Matriks identitas dilambangkan dengan huruf I. Bentuknya persegi yang semua elemen diagonal utamanya bernilai satu, dan elemen selain diagonal utama bernilai nol. Seperti ini bentuknya:

Matriks identitas punya peran yang cukup besar, misalnya mengubah koordinat dalam geometri, memecahkan sistem persamaan linier, dan mewakili grafik dalam teori graph. Elo bakal lihat contoh penerapannya di artikel yang gue tulis setelah ini >> Determinan Matriks dan Metode Penyelesaiannya.

Matriks Nol

Elo jangan heran ketika ada matriks yang semua elemennya bernilai nol. Ketika elo menemukan yang seperti itu, berarti elo ketemu sama jenis matriks nol. Yap, jenis yang satu ini semua elemennya bernilai nol, biasanya dilambangkan dengan huruf O (ordo).

Matriks segitiga

Matriks persegi yang elemennya membentuk segitiga. Matriks segitiga ini ada dua jenis, yaitu segitiga atas dan bawah. Untuk segitiga atas, elemen di bawah diagonal utamanya bernilai nol. Sedangkan segitiga bawah, elemen di atas diagonal utamanya adalah nol.

Segitiga Atas

Segitiga Bawah

Transpose Matriks

Suatu matriks yang diperoleh dari pertukaran baris dan kolom. Simpelnya, menukar baris jadi kolom, dan kolom jadi baris. Supaya lebih jelas, elo coba perhatikan gambar di bawah ini:

Matriks A setelah ditranspose akan berubah notasinya menjadi AT. Selain notasinya berubah, ordonya juga berubah ya, Sobat Zenius.

Operasi Matriks Matematika

Dalam matriks matematika ada beberapa operasi dasar yang perlu elo tau untuk memodifikasi matriks, seperti penjumlahan, pengurangan, dan perkalian.

Penjumlahan dan Pengurangan

Penjumlahan dan pengurangan pada matriks ini ada syaratnya lho. Syaratnya adalah ordo harus sama. Asalkan ukuran/ordonya sama (jumlah baris dan kolom sama), maka dua matriks bisa dijumlah dan dikurangi.

Cara menjumlahkan dan menguranginya memiliki prinsip yang sama, yaitu jumlahkan atau kurangkan elemen pada matriks A dengan matriks B yang letaknya sama. Coba perhatikan contoh di bawah ini:

Paham ya sampai sini? Untuk menguji pemahaman elo, sekarang cobain contoh soal berikut ini ya!

Perkalian baris dan kolom disebut dengan perkalian matriks. Eits tapi gak sesederhana itu, lho. Ada pembagiannya juga yang bisa elo lihat di bawah ini.

Perkalian dengan Bilangan Riil (Skalar)

Elo masih ingat gak apa itu bilangan riil atau skalar? Misalnya gini, elo punya matriks A, nah si matriks itu bakal elo kalikan dengan bilangan 3. Elo bisa menjumlahkan matriks A sebanyak 3 kali. Iya kan? Lebih jelasnya gini:

Tapi, ada cara cepatnya. Karena matriks ini bakal dikalikan sama bilangan skalar, elo tinggal kalikan aja bilangan skalar sama setiap elemen dalam matriks A.

Gampang lah yaa.. Intinya elo perlu ingat konsep perkalian bilangan skalar.

Coba elo kerjakan latihan soal berikut ini:

Perkalian Dua Matriks

Dua matriks bisa dikalikan apabila jumlah kolom pada matriks A sama dengan jumlah baris pada matriks B.

Caranya adalah tiap baris dikalikan dengan tiap kolom, terus dijumlahkan pada baris yang sama. Ah belibet, langsung aja deh ke contohnya biar jelas, meluncurrrr!

Sampai sini jelas ya? Perlu latihan soal matriks matematika gak supaya makin paham? Oke nih gue kasih.

Oke, segitu dulu pembahasan tentang pengenalan materi matriks matematika. Determinan dan invers matriks bakal gue bahas di artikel selanjutnya ya.

Oh iya, buat elo yang mau tau lebih lanjut tentang materu matriks matematika atau kalau masih bingung pembahasan lewat tulisan kayak gini, elo bisa banget tonton video materi Zenius di aplikasi Zenius.

Nggak perlu beli paket belajar tetap bisa kok nikmati video pembelajarannya. Tapi gue saranin elo untuk beli paket belajar Zenius, soalnya elo nggak bakal rugi karena bisa akses ke berbagai video premium, rangkuman pembelajaran, latihan soal hingga live class juga, lho. Yuk coba langganan paket belajar!

Tenang, buat bikin akun dan nonton videonya GRATIS kok. Nonton video materi matriks matematika di sini: Pengenalan Matriks dan Operasi Matriks. Kalau elo mau pelajari materi Matematika lainnya, langsung aja klik banner di bawah ini.