2000 tahun lalu Eratosthenes berhasil mengukur lingkar bumi dengan hanya menggunakan tongkat biasa. Mari kita buktikan dan lakukan sendiri percobaan itu.
Segala kecanggihan teknologi dan sains yang kita nikmati sekarang bisa dibilang berakar dari rasa ingin tahu (curiosity). Manusia mengamati lingkungan sekitarnya, membuat dugaan, melakukan eksperimen, dan menghasilkan sesuatu yang berguna. Dimulai dari eksperimen yang sederhana, sebuah pengetahuan akan diestafetkan dari zaman ke zaman untuk terus diperbarui. Pada artikel kali ini, gue ingin bercerita tentang sebuah eksperimen sederhana yang menjadi basis salah satu bidang ilmu pengetahuan hingga sekarang. Eksperimen ini dilakukan oleh Eratosthenes, seorang matematikawan Yunani kuno yang juga dikenal sebagai Bapak Geografi.
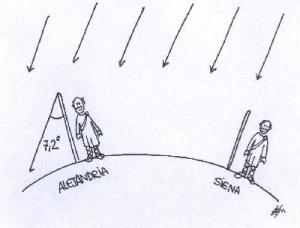
Pada tanggal 21 Juni sekitar 240 SM di siang hari, Eratosthenes yang saat itu berada di Siena, salah salah satu kota di Mesir yang sekarang bernama Aswan, melihat bahwa di dasar sebuah sumur, tidak ada bayangan yang terbentuk. Ia juga mencoba menegakkan sebuah tongkat. Tongkat yang berdiri tegak itu juga tidak menghasilkan bayangan. Namun, di saat yang bersamaan, hal ini tidak terjadi di Alexandria, kota di Mesir juga yang jaraknya 843 km dari Aswan. Di Alexandria, tongkat yang berdiri tegak menghasilkan bayangan. Bagi orang kebanyakan, hal ini mungkin dianggap sebagai fenomena umum sehari-hari. Tapi fenomena umum ini malah memancing curiosity seorang Eratosthenes.
Bagaimana bisa bayangan terbentuk di kota Alexandria, sedangkan di kota Aswan tidak?
Sekitar 100 tahun sebelum kejadian di atas, Aristoteles sudah membuktikan bahwa Bumi itu bulat, bukan datar. Perbedaan bayangan antara Alexandria dan Aswan hanya mungkin terjadi jika permukaan bumi melengkung. Eratosthenes lalu menyimpulkan bahwa matahari sedang tepat berada di atas kota Aswan. Oleh karena itu, ketika Eratosthenes melihat ada perbedaan sudut bayangan di Aswan dan di Alexandria, dia langsung mengambil kesempatan ini untuk mengukur lingkar Bumi.
Eksperimen Eratosthenes ini cukup terkenal karena ia bisa menghasilkan kalkulasi yang “hanya” meleset 15% dari pengukuran zaman modern menggunakan satelit. Tingkat akurasi tersebut lumayan impresif untuk ukuran manusia yang hidup 2000 tahun lalu yang hanya mengandalkan rasa ingin tahu dan sebuah tongkat sederhana. Eksperimen ini juga yang membuat Eratosthenes tercatat sebagai orang pertama yang mengkur lingkar Bumi.
Wah, gimana caranya tuh? Kira-kira, kita bisa mengulang percobaan yang sama nggak ya? Nah, di artikel ini, gue akan coba jelasin bagaimana Eratosthenes melakukan hal tersebut dan apa yang bisa kita lakukan nanti untuk melakukan percobaan serupa tanggal 4 Maret 2017 nanti. 🙂
Eratosthenes mengukur lingkar Bumi
Eratosthenes melaporkan pengukuran ini di buku “On the measurement of the Earth”. Cuma sayangnya, buku tersebut sudah hilang. Jadi, kita tidak tahu persis bagaimana cara Eratosthenes melakukan hal tersebut. Informasi terkait teknik yang dilakukan Eratosthenes ini kita dapatkan dari (1) buku-buku lain yang merujuk ke buku yang ditulis Eratosthenes ini dan (2) dugaan yang masuk akal terkait bagaimana Erathosthenes bisa melakukannya. Apa yang akan gue tuliskan di artikel ini adalah campuran dari keduanya. So, bagaimana cara Eratosthenes mengukur lingkar Bumi?
Di kota Aswan (Siena), bayangan tidak terbentuk karena sinar matahari tegak lurus dengan permukaan bumi. Sementara di kota Alexandria, sinar matahari tidak tegak lurus dengan permukaan bumi. Sudut antara tongkat dan bayangan bisa dicari. Eratosthenes mendapatkan bahwa sudutnya adalah sebesar 7,2o.
Image credit: todaslascosasdeanthony.com
Kalau tongkat di Alexandria dan di Aswan tersebut kita tarik garis lurus sampai dengan pusat Bumi, kira-kira kita akan mendapatkan gambar seperti berikut ini:
Dengan menggunakan prinsip sudut sehadap dan bertolak-belakang, kita bisa mendapatkan bahwa sudut antara kota Alexandria dan kota Aswan juga sama dengan 7,2o.
Sampai sini kira-kira kebayang nggak apa yang berikutnya harus dilakuin oleh Eratosthenes untuk bisa menghitung keliling Bumi? Kalau belum kebayang, perhatikan gambar berikut ini:
Keliling itu bisa dicari dengan persamaan berikut ini:
Intinya, perbandingan antara sudut 7,2o dengan 360o sama dengan perbandingan antara L dan keliling. Kalau begitu, tinggal kita hitung aja berapa nilai L. Pada kasus Eratosthenes ini, L adalah jarak dari kota Alexandia ke kota Aswan. Jadi, yang berikutnya harus dia lakukan adalah mengukur jarak kedua kota tersebut.
Eratosthenes dikabarkan membayar orang untuk berpergian dengan unta untuk mengukur jarak antara kedua kota tersebut. Dia mendapatkan jaraknya adalah 5000 stadia (sekitar 925 km). Dengan demikian, dia bisa memasukkan angka ini ke dalam rumus di atas. Hasilnya adalah sebagai berikut:
Kalau kita bandingkan dengan keliling bumi yang diukur di zaman modern (40.075 km), perhitungan Eratosthenes ini cuma meleset sekitar 15%. Salah satu penyebab melesetnya itu adalah karena data yang kurang akurat. Sebagai contoh, jarak antara kedua kota tersebut sebenarnya bukan 925 km, tapi 843 km. Kemudian sudut kedua kota tersebut juga bukan 7,2o, tapi 7,76o. Seandainya Eratosthenes menggunakan data yang lebih akurat dalam menghitungnya, maka dia akan mendapatkan hasil 39.108 km. Hanya meleset 2,4% dari keliling bumi yang diukur di zaman modern.
Mengulang Pengukuran Eratosthenes
Kalau lu tertarik, gue mau mengajak lu untuk melakukan pengukuran serupa dengan yang dilakukan Eratosthenes nih. Supaya kita bisa melakukannya bareng-bareng, gimana kalau kita tetapin aja tanggalnya, Sabtu ini, 4 Maret 2017. Menurut situs ini, pada tanggal tersebut, pukul 12.04, matahari akan berada pada koordinat 6,36o LS (Lintang Selatan) dan 106,85o BT (Bujur Timur). Lokasi yang nggak jauh dari koordinat tersebut adalah di kampus UI Depok (6,36o LS 106,83o BT).
So, pada tanggal itu, gue mungkin akan berada di sekitar UI Depok untuk memastikan bahwa tidak ada bayangan yang terbentuk di situ sekitar pukul 12.04. Gue akan melihat bahwa panjang bayangan di situ adalah nol, seperti fenomena yang terjadi di kota Aswan di zaman Eratosthenes.
Nah, terus siapa yang berada di “Alexandria” untuk melakukan pengukuran sudutnya? Well, kali ini gue mau minta bantuan dari para pembaca artikel ini. Kalau lo tertarik untuk ikutan dalam proses pengukuran ini, coba lakukan langkah-langkah berikut ini pada Sabtu ini, 4 Maret 2017:
- Ambil tongkat. Ukur panjang tongkat tersebut.
- Tegakkan posisi tongkat tersebut di lapangan. (Bisa pakai semacam bandul untuk memastikan bahwa posisi tongkat sudah tegak).
- Pada pukul 12.03, 12.04, dan 12.05 WIB, ukur panjang bayangan yang terbentuk. Pengukuran dilakukan pada 3 waktu untuk jaga-jaga aja sih. Bisa jadi matahari tepat di atas UI Depok bukan 12.04, tapi 12.03 atau 12.05 WIB.
- Buka Google Maps, coba cek berapa koordinat tempat lu melakukan pengukuran tersebut (dalam Lintang Utara/Selatan dan Bujur Timur). Caranya, klik titik/posisi lo berdiri pada map untuk memunculkan informasi koordinat.
Setelah data-data yang dibutuhkan sudah terkumpul, berikutnya adalah melakukan perhitungan. Cuma butuh dua perhitungan kok, yaitu perhitungan sudut dan perhitungan jarak. Gimana cara menghitung keduanya?
1. Menghitung sudut
Sudut yang dicari adalah sudut yang terbentuk antara tongkat dan bayangan seperti gambar berikut ini:
Kita bisa mencari besar sudut dengan persamaan:
Kalau nilai tangen-nya sudah didapat, bisa lah ya mencari nilai sudutnya?
2. Menghitung jarak
Kalau kita mau mengukur jaraknya secara langsung, ini agak berat sih. Karena itu artinya lo harus bepergian dari UI Depok ke lokasi lo melakukan pengukuran. Dan bepergiannya itu harus garis lurus. Kalau belok-belok, pengukurannya jadi nggak tepat.
Nah, daripada kita mengukur langsung, lebih baik kita pakai bantuan aja untuk menghitung jaraknya. Setidaknya ada dua cara untuk melakukan ini.
Cara pertama: Menggunakan software penghitung jarak
Lo bisa menggunakan website ini misalnya untuk menghitung jarak antara dua lokasi. Tinggal masukkan aja koordinat kedua lokasi, lalu website tersebut akan memberikan laporan jaraknya. Tapi kita harus melakukan konversi koordinatnya dulu ya. Sebagai contoh:
Koordinat UI Depok adalah di 6,36o LS 106,83o BT. Sebelum kita input di website tersebut, kita konversi dulu menjadi begini:
- Lintang (Latitude) : 6o 21’ 36” S
- Bujur (Longitude) : 106o 49’ 48” E
Kelebihan dari cara ini adalah lebih simpel, lebih akurat, dan lebih presisi. Tapi ini sebenernya agak “curang”. Karena software di website tersebut menggunakan informasi keliling dan jari-jari bumi untuk menghitung jarak. Padahal itu yang mau kita cari tahu. Oleh karena itu, gue merekomendasikan supaya lo juga menghitung dengan cara kedua.
Cara kedua: Mengukur di peta
Ambil sembarang peta. Ukur jarak antara keduanya dengan menggunakan alat ukur (penggaris atau apapun). Kemudian hitung jarak sebenarnya dengan menggunakan informasi skala yang tertera pada peta. Nggak terlalu susah juga kan pakai cara ini? 🙂
3. Menghitung keliling Bumi
Kalau jarak dan sudut sudah diketahui, kita tinggal masukkan angka-angka yang udah lo dapet ke persamaan berikut ini:
Dengan θ dan L adalah sudut yang jarak yang baru aja lo hitung.
Setelah lo melakukan pengukuran dan perhitungan di atas, jangan lupa kabari hasilnya di komentar di bawah ya. Kalau hasil perhitungannya agak jauh dari 40.075 km, nggak masalah sih. Laporkan apa adanya aja. Toh hasil perhitungan Eratosthenes juga nggak segitu kok.
Okay, gue tunggu laporan dari lu di komentar di bawah ya 🙂
Update: Hasil Pengukuran
Seperti yang sudah dijanjiin sebelumnya, gue dan beberapa orang dari tim Zenius datang ke Aswan* untuk menyaksikan hilangnya bayangan pada hari Sabtu, 4 Maret 2017, Pukul 12:04.
*) Maksudnya ke Taman Balairung di Universitas Indonesia, Depok. Hehe.
Mulai jam 12 pas, proses hilangnya bayangan ini kita siarkan LIVE di Instagram Zenius Education. Tepat pada pukul 12:04, bayangannya hilang seperti foto di bawah ini:
Pada waktu yang sama di berbagai tempat lainnya, beberapa anak (yang awesome banget) ikutan dalam proses pengukuran lingkar bumi ini. Ada yang di Melbourne, Purwokerto, Surabaya, Batu, Lampung, dan lain-lain. Mereka semua melaporkan via komentar di artikel ini atau di social media. Seluruh laporan tersebut sudah gue kompilasi di tabel di bawah ini.
Catatan: Pengukuran di Purwokerto errornya jauh banget. Kabarnya sih di sana Mendung pada saat pengukuran. Ada dua yang dari Purwokerto dan perbedaan antara keduanya lumayan jauh juga.
Selain yang melaporkan di atas, ada juga yang sudah berusaha mengukur tapi gagal karena alasan cuaca (mendung, hujan, atau matahari tertutup awan). Terlepas dari itu semua, thanks berat untuk ikutan dalam proses pengukuran lingkar bumi ini. You are awesome! 🙂
Keren.kak
Btw saya mw nanyak ni kak.
Kira2 berapa biaya yang dibutuhkan untuk mengikuti program belajar langsung di zenius ya kak? Mohon infonya ya kak☺
Thanks Tomy. 🙂
Informasi mengenati harga voucher bisa dilihat di image di bawah. Kalau mau beli, bisa langsung ke halaman berikut ini:
https://www.zenius.net/voucher-purchase-online
https://uploads.disquscdn.com/images/b1f5b851f1c02467528125d4a6ed2d6da48031ba98fa0bc2e4fbffe2e34eee15.png
Kak wisnu materi kelas 11 SMA kurikulum 2013 belum di update lagi yaa? Btw materi di sekolah saya dengan di zenius ada yang beda?
beda gimana ini maksudnya?
Materi yang di buku saya gaada di zenius.net kak?
Bab apa aja yang nggak ada di zenius.net? Di sekolah pakai kurikulum 2013 yang lama atau kurikulum 2013 yang sudah direvisi? Di zenius.net ada dua2nya. Untuk persiapan UTS semester genapnya, sabar yah. Sedang kita persiapkan. 🙂
Halo klw info untuk ikut bimbel zenisus-x gmn ya kak. Mohon infonya?
Oh, kalau bimbel zenius-X udah nggak ada. Sekarang adanya zenius center.
Bang .Kira2 klw baru belajar dari sekarang bisa nggak ya bang? . Sementara sbmptn udh h-70 an?
.
Kereeeen kak ?
Btw aku mau request nih kak bisa tolong bahas ttg konsep aljabar ga?
Aku blm dpt esensi nya nih kak belajar aljabar linier sm struktur aljabar. Pengen tau manfaat sm serunya belajar itu tuh apa sih ?
Ditunggu bgt loh kak hehe
Thanks Alysa. 🙂
Konsep aljabar itu luas banget. Hampir semua materi matematika SMA itu ada aljabarnya. Untuk review singkat, di zenius.net ada sih, yaitu di basic mathematical skills. Tapi kayaknya materi yang lu maksud itu materi perkuliahan ya? (aljabar linier dan struktur aljabar). Kalau itu nggak kita bikin.
Kak.. bahas tentang trik2 matematika sma dong sesekali.. biar mudahin operasi2 natematika sma.. ps: fisika juga boleh
Trik matematika yang kayak apa yang dimaksud? Yang kayak gini atau gini? Atau yang lebih deket ke pelajaran seperti yang kayak gini? Fisika juga ada di sini, di sini, dll. Semua link barusan itu link ke artikel blog. Kalau matematika yang terkait sama kurikulum, itu semua ada di video di zenius.net. Kalau mau lihat beberapa reviewnya, cek basic mathematical skills juga bisa.
ini kalo saya ga salah yah. itu untuk menghitung sudut pake tan kan nah kok pangjang bayangan dibagi panjang tongkatnya. kalo kita jadikan x sebagai pangjang bayangan dan y sebagai panjang tongkat seharusnya kalo tan = y/x dong kalo itu mah jadi ctg dong bener ga nih CMIIW.
Oh. Nilai tan itu y/x kalau sudutnya yang kiri bawah (depan dibagi samping). Kali ini kan sudut yang dicari ada di atas. Jadi depannya sudut itu adalah panjang bayangannya, sementara sampingnya sudut itu adalah panjang tongkatnya.
oh iyah bener sudutnya ada diatas. karna kebiasaan juga sih, maafkan
Siip. Nggak apa-apa, gue juga kadang suka nggak teliti kok. Hehe.
gimana caranya eratosthenes bisa tahu di kota alexandria ada bayangan sementara dia lagi di aswan?
nah, ini juga yg aku tanyain.
kedua kota kan jaraknya jauh, gimana caranya dia dapet sudut tsb krn seharusnya sudut tsb diukur pd waktu bersamaan
Good question nih. Pertama-tama, gue tekankan dulu bahwa buku yang ditulis langsung Eratosthenes itu sudah hilang ya. Jadi, kita nggak bisa tahu persis. Sejauh ini, dugaan kita itu begini: setelah dia mengetahui tanggal berapa matahari berada tepat di atas Aswan, dia pergi ke Alexandria tepat pada tanggal itu juga (di tahun berikutnya mungkin). Di sana, dia baru melakukan pengukuran seperti yang dijelaskan di artikel di atas.
Kak.. pengen dibahas dong tentang bumi itu bulat atau datar.. hehe mohon pencerahannya karena banyak dibahas di youtube (katanya) bumi itu datar.
Kalau itu udah pernah dibahas. 🙂
Kak, untuk melakukan pengamatan ini sinar matahari harus tegak lurus dengan permukaan salah satu tempat, atau bisa aja kedua permukaan tempat yang diamati tidak tegak lurus dengan sinar matahari?
Iya, untuk bisa mengukur seperti Eratosthenes, matahari harus tepat di atas salah satu tempat. Kalau enggak, nanti kita bisa mengukur lingkaran yang salah. Inget, bumi itu seperti bola. Lingkaran yang kita ukur itu harus lingkaran yang tengah-tengahnya berada di pusat bola.
Oke kak, aku udah dapat poinnya. Terus, bumi itu kan gak bulat sempurna, jadi lingkaran – lingkaran yang pusatnya sama-sama pusat bumi belum tentu punya keliling yang sama. Jadi, keliling lingkaran mana yang dimaksud keliling bumi?
Menurut info di Wikipedia, meskipun bumi itu nggak bulat sempurna, tapi pendekatan bulat sempurna itu juga lumayan akurat kok. Berdasarkan pengukuran terkini, keliling bumi di Ekuator dan di Meridian itu cuma beda tipis, di bawah 1%.
Equatorial: 40.075,017 km
Meridional: 40.007,86 km
Pengukurannya bisa seteliti itu karena pakai satelit. Kalau pakai metode Eratosthenes sih gue rasa errornya pasti lebih dari 1%, jadi nggak ada bedanya lo mengukur di Ekuator ataupun di Meridian.
beuhhh mantap jiwa bang wisnuuu
Thank you. Besok ikutan ngukur nggak? 🙂
Keren kakak, jadi lebih tertarik ambil yg berhubungan dg geografi nanti waktu kuliah, hehe skrg aku ambil ipa karena nnti katanya kalo geografi non pendidikan masuk saintek ya.. Dari kecil saya suka sama hal2 yg berhubungan dgn bumi. Waktu kecil suka banget geografi, suka baca ensiklopedia, majalah national geographic, atlas dan mainin tuh globe sampe hapal persis letak negara2 dan profil nya wkwk.
Thanks Tieto. Lo tinggal di mana btw? Ikutan ngukur ya terus nanti laporin hasil pengukurannya di sini. Hehe.
Surabaya kak, sudah tak ukur barusan pada pukul 12.03-12.05, ±
-panjang bayangan: 20 cm (0,2 m)
-panjang tongkat: 120 cm (1,2m)
Koordinat:
LS (Latitude): 7° 18′ 22″ S
BT (Longitude): 112° 43′ 58″ E
Aku pake aplikasi yg dikasih di blog zenius ya kak, jadinya jaraknya gini 660,01 km
https://uploads.disquscdn.com/images/11a5feede10c69f037e8c9485e35c5655e7e809fd269f2dce5bd49930ae5be3b.png ..
hehe.. kalo pake jarak terdekat beda sih hasilnya sama jarak tempuh sebenarnya ya kan kak? Kalo sebenarnya mungkin hampir ±900 km, karena faktor jalannya, ada yg belok, dsb spt d maps:
https://uploads.disquscdn.com/images/bef015039baea5dc0814742394199bdded809fadfd4e442ae5a5f958c1a4e71c.png
Sudah dihitung lagi, tapi kenapa kok meleset ya? Mungkin karena emang manual, melesetnya juga ± 10-15%, cuma ini lebih kecil..
Tan=120÷14= 6,65°
K=360°÷6,65°x660km= 35.729km
Mantap nih. Melesetnya sekitar 11%. Nggak masalah sih. Masih lebih akurat dibanding hasil pengukuran Eratosthenes. Hehe… Top!
questions:
1. apakah metode pembuktian di atas akan berlaku jika buminya datar? mengingat diatas tidak dijelaskan atau minimal ada preview tentang asumsi bumi ini bulat.
2. jika pun buminya bulat, apakah pengujian dengan hanya 2 titik yang dilakukan aritosthenes itu sudah cukup? mengingat cahaya matahari yang sampai ke bumi itu menyebar maka jika buminya datar pun akan bisa dipastikan satu titik yang tepat di bawah matahari tidak akan ada bayangan dan di titik lain akan dipastikan memiliki bayangan.
3. apakah panjang tongkat berpengaruh terhadap sudut yang dihasilkan? mengingat panjang bayangan yang dihasilkan juga pasti akan berbeda
CMIIW, just asking..
1. Ada dua asumsi dasar dalam percobaan Eratosthenes ini. Pertama, bumi itu bulat sempurna. Ke dua, jarak matahari ke bumi itu begitu jauh sehingga bisa dianggap tak hingga (sinarnya sejajar). Dalam percobaan ini, Eratosthenes sebenernya tidak membuktikan bahwa bumi itu datar lagi sih. Bukti itu udah pernah disebutin Aristotles 100 tahun sebelumnya.
2. Yup. Udah cukup. Karena asumsi yang ke dua itu. Itu asumsi yang lumayan valid karena jarak matahari ke bumi memang jauh buanget.
3. Panjang tongkat hampir nggak ada pengaruhnya sama sekali. Karena yang kita ukur di sini bukan panjang tongkatnya, melainkan rasio antara panjang tongkat dengan panjang bayangan (nilai tangen). Rasionya itu akan sama saja mau pakai tongkat yang pendek maupun yang panjang. Cuma kalau tongkatnya terlalu pendek, pengukurannya jadi kurang teliti.
SIEVE OF ERATHOSTENES
Hehe… bilangan prima ya?
Bang, posisi gue di Bandung. Emang belum mulai sih percobaan ngukur keliling bumi, cuman barusan gue coba2 doang liat bayangan tongkat eh panjang bayangannya tuh pendek bgt. Gatau berapa sih pokonya pendek. Kira2 yaa 10cm ada lah. Naah apa mungkin sebelumnya sinar matahari tegak lurus dengan tempat gue barusan? Atau bukan sebelum tapi beberapa menit lagi? Duuh gue ngomongnya jelimet huhuuu
Kalau di Bandung hari ini sih harusnya matahari nggak akan tepat di atas. Terus akhirnya tetep ngukur nggak di pk. 12:04? Kalau ngukur, laporin hasil pengukurannya yah.
kak, aku barusan ngitung dapatnya 33.363,3216 km kok mlesetnya lumayan jauh ya wkwk
coba diuraikan berapa panjang tongkatnya, berapa cm bayangannya, dan koordinat lokasi waktu pengukuran kamu
Panjang tongkat : 111 cm
Panjang bayangan : 12,5 cm
Koordinat lokasi waktu : 8°02’10.07″S 111°57’29.09″E
itu kak,
Mantap nih. Udah OK kok. Perhitungannya juga bener. Meleset 11% itu nggak masalah. Masih lebih akurat dibanding pengukurannya Eratosthenes. 🙂
panjang tongkat = 170 cm
panjang bayangan (12:13) = 21.5 cm
sudut terbentuk = arctan(21.5/170) = 7.207963 deg
jarak terdekat dari ui ke rumah = 13.5 km
lingkar bumi = 360 deg/7.207963 deg * 13.5 km = 38631.92269 km
Thank you laporannya, Hakan. Cuma ngukurnya nggak pas di 12:04 ya? Tapi di 12:13. Itu hasil perhitungannya juga jadi salah. 360×13,5/7,2 itu bukan segitu, tapi 674 km.
iya sama2. iya tadi ga diwaktu yg pas soalnya ngeliat live ig dulu baru coba wkwk. bener sih perhitungannya jadi salah, kalo derajatnya diubah ke radian. kayaknya panjang bayangan di tempat situ harusnya 0.37cman baru agak bener perhitungannya
Iya lagi pula jaraknya terlalu deket (13,5 km). Semakin dekat jaraknya, semakin besar juga kemungkinan errornya sih.
Uda gue coba bang. Gatau tongkatnya lurus aoa engga. Wkwk. Tapi tongkat e kayak e lurus sih.
Hasilnya
Ukuran tongkat 95cm
Ukuran bayangan 8 cm
Daerah solo bang jawa tengah.
Gue gatau cara amvbil koorfinat wkwkw
tinggal open google map location aja kok, kalo ada keterangan koordinat lokasinya 🙂
Barusan gue cek di Google Map koordinatnya Stasiun Balapan solo itu:
7 33′ 36″S
110 49′ 12″E
Anggap nggak jauh dari situ lah ya?
Berarti kalau gitu jaraknya dari UI adalah sekitar 460,2 km. Dari pengukuran ukuran tongkat dan bayangan, didapat sudutnya 4,81 derajat. Kelilingnya adalah = 34.418 km. Mantap sih ini, cuma meleset 14%. Cool. 🙂
Panjang Tongkat = 50 cmBayangan = 2 cm
tan x = 2/50
x = 2,29°
Keliling = (360°/2,29°) x 248,50 km = 39065,5 km
@wisnuops:disqus , Nyaris kak ? ? ?
Keren. Bisa share koordinatnya juga supaya bisa gue cek hasil perhitungannya? (cek pakai google map aja)
-5.223357, 104.902063
5°13’24.1″S
104°54’07.4″E
bang , gue ukur dari kota batu tadi ketemu 39769,3 KM ,
panjang tongkat 31cm , panjang bayangan 3,2 cm , tp gue nggak tau koordinat disini , tapi gue tadi browsing dapet koordinatnya segini 105° 9′ 5.567″ , dan jarak batu depok sekitar 650,67 km , bener gak ? wkwkwk
Kalau alun-alun kota batu gue dapetnya -7,87 dan 112,53 di Google Map, atau sama dengan:
7 52 12S
112 31 48E
Yang artinya jaraknya 650.9 km dari UI. Yah, nggak jauh lah dari perhitungan lu. Keliling Buminya sekitar 39,760. Ini errornya cuma 1%, termasuk yang kecil banget.
Kak mau nanya, sebaiknya beli xpedia yang alumni atau untuk kelas 12 (saya masih kelas 11) tapi pengen belajar sbm dr sekarang. Kalau beli sekarang voucher untuk zenius.netnya berlaku sampai kapan ya kak? Mohon di respon kak thankss
bang kok gue hasilnya jauh banget ya?
hasilnya kek gini.
lokasi rumah gue di purwokerto, ordinatnya 7o 22′ 27.323″ S & 109o 9′ 24.048″ E
jarak rumah gue ke jakarta 280,5 Km. tongkat yang gue pake(TBH, besi) ukurannya 120 Cm, ngamatinnya pas jam 12:02 kemaren. hasil bayangannya 2 Cm.
Kalau bayangannya sependek itu, kemiringan tongkat sedikit aja udah bisa menggeser panjang bayangan lumayan jauh. Beberapa hal yang mungkin perlu diperhatikan pada saat pengukuran:
1. Apakah tongkat sudah benar-benar tegak? Perlu dicek pakai bandul (tali, ada beban di bawahnya). Apakah tongkat sudah lurus dengan bandul tersebut?
2. Berapa diameter dari tongkat? Apakah bayangan diukur dari tengah-tengah tongkat atau dari pinggir tongkat. Kalau diameter tongkatnya besar (4 cm misalnya), terus lo mengukur dari pinggir tongkat 2 cm, berarti harusnya kan laporannya 4 cm. Itu udah beda 2x lipat. Jauh banget kan?
Sebagai perbandingan, kemarin ada yang melaporkan pengukuran dari Purwokerto juga. Panjang tongkatnya 121 cm (mirip sama lu), tapi panjang bayangannya 8 cm. Beda lumayan jauh kan? Kalau di dalam satu kote perbedaannya bisa sejauh itu, kemungkinan besar salah satu dari kalian teknik ngukurnya ada yang salah.
Thanks bang, masukannya. Tbh, kemarin itu Purwokerto daerahku beneran mendung, bahkan ujan sekitar jam 1an. Jadi mungkin emg salah pada pengukurannya.
Oh, iya. Infoin lagi ya bang, biar bisa nge buktiin bareng2. Terutama mau benerin cara ngikutin lagi. ?
Kalau mau ngukur sendiri sebenernya bisa-bisa aja sih. Sebagai contoh, menurut situs ini, besok 8 Mar 2017 jam 12 pas, matahari akan berada di 4° 49′ lintang selatan dan 107° 42′ bujur timur. Tinggal lakukan aja eksperiman yang sama di purwokerto pada waktu tersebut.
Kemarin kita ngukur bareng-bareng supaya ada orang yang meng-konformasi bahwa beneran di koordinat tersebut, matahari tepat berada di atas.
Wisnu, eksperimennya Eratosthenes di atas juga dijabarkan di buku Cosmos-nya Carl Sagan ya? *baru ngeh
Yoi.
bang debunk tryphophobia dong
The Earth is Flat!!!
@wisnu OPS tolong diupdate buat pelajaran bahasa inggris dan indonesia buat kelas 8 kurtilas thks
meleset 15% masih kalah sama Al-Biruni 🙂
Kelamaan mengetahui panjang keliling bumi dengan ngukur bayang2..
Begini aja.. kita ketahui kecepatan bumi 1770km/jam
Katanya keliling bumi berkisar 40075km
Kita buktikan dengan perbandingan kecepatan rotasi bumi.
Begini caranya 1770km/jam di kalikan dengan 1 hari=24 jam bumi berputar pada porosnya kembali ke titik awal. Jadi hasil perkaliannya = 1770×24=42480km
Jadi keliling bumi = 42480km
Jika benar keliling bumi itu 40075km
Maka seharusnya kecepatan rotasi bumi 1669,98km/jam
Sebenarnya data yang akurat itu yang mana… Apa kita hanya di bodohi dengan angka… Atau kita di bodohi dengan rumus…
Bukti bumi bulat tidak bisa diperoleh dgn cara ini, dgn asumsi bumi datar pun akan tampak sudut sebesar itu
Bagaimana eratothenes mengukur pusat bumi. Sehingga didapati sudut 7°
Tpi bukankah ada perbedaan ukuran keliling bumi jika diukur secara vertikal, bila di bagian horizontal adalah khatulistiwa. Soalnya kan bentuk bumi tidaklah bulat sempurna.
bang izin ngambil data perhitungannya ya
Keren kak…
Mau tanya kak… Bagaimana komunikasinya ya kak dari kota Alexandria dan kota Aswan dengan jarak 843 km pada waktu yg sama… itu terjadi pada tanggal 21 juni 240 sm…???
Menurut data? Asumsi? atau persamaan?
Nanya dong, kalo percobaan kayak gini bisa diulang setiap waktu nggak?
pertanyaannya adalah pada saat itu bagaimana dia bisa tahu pada saat bersamaan di di Alexandria tongkatnya ada bayangan padahal saat itu dia di sienna melihat tongkat yg tidak ada bayangan ? apakah ada temannya di alexandria yg kirim WA ?