Peluang Kejadian Saling Bebas - Materi Matematika Kelas 12

Hai guys, kali ini gue mau ngebahas peluang kejadian saling bebas, nih. Pernah denger, nggak? Apa itu dan kayak gimana contohnya, langsung aja kita kupas bersama dalam artikel ini, yuk!
Konsep Kejadian Saling Bebas
Peluang kejadian saling bebas bisa juga disebut sebagai peluang kejadian independen. Biar elo gampang ngebayanginnya, gue ada sebuah ilustrasi. Misalnya seorang guru hendak memilih masing-masing 2 murid dari kelas A dan B untuk diikutsertakan dalam lomba Sains dan pidato Bahasa Inggris.

Misalnya di kelas A udah terpilih satu orang untuk lomba Sains. Maka, peluang seorang murid untuk terpilih jadi peserta lomba pidato jadi terpengaruh, jumlah total siswa dikurangi satu karena sebelumnya seorang udah diikutkan lomba Sains. Makanya, kejadian ini disebut sebagai peluang kejadian dependen.
Baca Juga: Rumus Peluang dan Aplikasinya dalam Kehidupan Sehari hari
Gimana dengan kelas B? Kalau di kelas A udah ada yang terpilih, ada pengaruhnya nggak, ya, dengan peluang di kelas B? Jawabannya adalah nggak! Ini merupakan salah satu contoh peluang kejadian saling bebas atau independen. Elo bisa nonton video belajar Zenius yang menjabarkan contoh ini dengan klik banner di bawah ini!
Kesimpulannya, kejadian saling bebas adalah dua kejadian yang tidak saling mempengaruhi kejadian lain. Kalau dirumuskan, jika A dan B saling bebas maka peluangnya adalah:
P(A∩B) = P(A) ⋅ P(B)
Contoh Kejadian Saling Bebas
Nah, sekarang elo udah paham konsepnya kan? Biar pemahaman elo tambah dalem kayak Samudra Pasifik, gue kasih contoh soal peluang kejadian saling bebas beserta pembahasannya buat elo pelajari.

Sebuah kota memiliki dua mobil pemadam kebakaran yang beroperasi bebas satu sama lain. Peluang kedua mobil tersebut tersedia ketika diperlukan adalah 0,16 dan peluang salah satu mobil tersedia ketika diperlukan adalah 0,5.
Tentukan:
a. Peluang mobil lainnya tersedia ketika diperlukan
b. Peluang salah satu mobil tersedia ketika keduanya diperlukan
Coba diteliti soalnya dulu, ya … udah? Oke, sekarang yuk kita masuk ke pembahasan! Pertama-tama, kita bikin perumpamaan dulu biar ngerjainnya lebih gampang. Umpama kejadian mobil 1 tersedia adalah A dan mobil 2 tersedia adalah B.
Menurut soal, katanya peluang kedua mobil atau P(A∩B) nya adalah 0,16, sedangkan peluang salah satu mobil tersedia adalah 0,5. Kita anggap aja kalau P(A) nya itu 0,5, ya. Karena kejadiannya saling bebas, maka:
P(A∩B) = P(A) ⋅ P(B)
0,16 = 0,5 ⋅ P(B)
P(B) = 0,32
Jadi, peluang mobil lainnya tersedia ketika diperlukan adalah 0,32. Poin a udah terjawab ya, gampang kan? Oke, kita lanjut ke poin b!

Kalau ngomongin tentang peluang salah satu mobil tersedia ketika keduanya diperlukan, maka akan ada dua kemungkinan nih:
I. Mobil 1 tersedia (A) dan mobil 2 tidak tersedia (C)
II. Mobil 1 tidak tersedia (D) dan mobil 2 tersedia (B)
Di sini, kejadian D merupakan komplemen dari kejadian A sedangkan kejadian C merupakan komplemen dari kejadian B. Karena kita mau nyari peluang salah satu mobil tersedia, kita akan menggabungkan kemungkinan I dengan kemungkinan II. Jadi,
P(IUII) = P(I) + P(II) – P(I∩II)
Nah, karena kejadian I dan II merupakan kejadian saling lepas, jadi nggak ada irisannya. Maka P(I∩II) = 0, kita hilangin aja, ya! Jadi,
P(IUII) = P(I) + P(II)
P(IUII) = P(A) ⋅ P(C) + P(D) ⋅ P(B)
Perlu diingat,
P(C) kan komplemen dari P(B), jadinya P(C) = 1 – P(B).
Begitu juga dengan P(D) yang merupakan komplemen dari P(A), P(D) = 1 – P(A). Jadi,
P(IUII) = P(A) ⋅ P(C) + P(D) ⋅ P(B)
P(IUII) = P(A) ⋅ (1-p(B)) + (1-P(A)) ⋅ P(B)
P(IUII) = 0,5 ⋅ (1-0,32) + (1-0,5) ⋅ (0,32)
P(IUII) = 0,5
Jadi, peluang salah satu mobil tersedia ketika keduanya diperlukan adalah 0,5.
Baca Juga: Pengertian Galat dan Contohnya dalam Kehidupan Sehari-hari – Materi Matematika Kelas 12
Gimana, udah paham belum? Elo bisa nonton video pembahasan soal ini lebih jauh di sini. Sekarang sebelum gue akhiri artikel ini, kita coba asah kemampuan elo dengan kerjain beberapa contoh soal, yuk!
Contoh Soal Peluang Kejadian Saling Bebas
- Misalnya P dan Q adalah dua kejadian saling bebas. Peluang P adalah 2/5 dan peluang Q adalah 1/4. Hasil dari P(P∩Q) adalah .…
a. 1/10
b. 3/20
c. 1/5
d. 4/5 - Sebuah koin dan dadu dilempar secara bersamaan. Peluang munculnya gambar pada koin dan angka pada dadu adalah ….
a. 1/2
b. 1/12
c. 1/3
d. 1/6
e. 1/4 - Dalam sebuah kantong A yang berisi 8 buah mangga, 2 buah mangga di antaranya busuk, sedangkan dalam kantong B yang berisi 10 buah apel, 5 di antaranya busuk. Ibu ingin mengambil 4 buah mangga dan 3 buah apel. Peluang terambilnya mangga dan apel yang tidak busuk adalah ….
a. 1/56
b. 2/156
c. 3/56
d. 4/56
e. 5/56
Pembahasan
- Jawaban: a.
Diketahui
P(P) = 2/5
P(Q) = 1/4
Karena P dan Q adalah dua kejadian saling bebas, maka P(P∩Q):
P(P∩Q) = P(P) ⋅ P(Q) = 2/5 ⋅ 1/4 = 1/10 - Jawaban: e.
Misalkan A merupakan munculnya gambar pada koin dan B merupakan munculnya angka ganjil pada dadu. Maka dari soal dapat ditentukan:
P(A) = 1/2
P(B) = 3/6 = 1/2
Munculnya gambar pada koin dan munculnya angka ganjil pada dadu adalah kejadian saling bebas, maka:
P(A∩B) = P(A) ⋅ P(B) = 1/2 ⋅ 1/2 = 1/4
Jadi, peluang munculnya gambar pada koin dan angka ganjil pada dadu adalah 1/4. - Jawaban: a.
Misalnya M merupakan terambilnya buah mangga yang tidak busuk dan A merupakan terambilnya buah apel yang tidak busuk.
Dari 8 buah mangga, ada 2 yang busuk dan 6 yang tidak busuk. Maka,

Dari 10 buah apel, terdapat 5 yang busuk dan 5 yang tidak busuk. Maka,
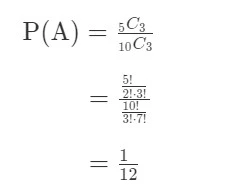
Peluang terambilnya 4 buah mangga yang tidak busuk dan 3 buah apel yang tidak busuk adalah
P(M∩A) = P(M) ⋅ P(A) = 3/14 ⋅ 1/12 = 1/56
Oke deh, sekian untuk materi peluang kejadian saling bebas. Sampai ketemu di artikel lainnya!
Baca Juga: Pengertian Teorema Bayes dan Contoh Soalnya – Materi Matematika Kelas 12




