Integral Parsial dan Integral Substitusi - Materi Matematika Kelas 11
Sobat Zenius, ketika elo naik ke kelas 11, elo bakalan bertemu dengan rumus integral parsial dan rumus integral substitusi.
“Aduh, pusing nih sama aljabar!”
Eits, jangan khawatir. Kita bisa belajar dan bahas contoh soalnya bareng-bareng!
Pengertian Integral Parsial
Integral parsial adalah teknik penyelesaian persamaan integral dengan pemisalan. Ini karena komponen yang akan diintegralkan memuat variabel yang sama meski memiliki fungsi yang berbeda.
Kira-kira, skemanya seperti tabel berikut.
Download Aplikasi Zenius
Tingkatin hasil belajar lewat kumpulan video materi dan ribuan contoh soal di Zenius. Maksimaln persiapanmu sekarang juga!
Rumus Integral Parsial
Biasanya, rumus integral parsial digunakan untuk menyelesaikan persamaan kompleks. Berikut rumusnya:
Keterangan masing-masing variabel ini adalah:
u=f(x), sehingga du=f(x)dx
dv=g(x)dx, sehingga v=g(x)dx
Apabila f(x) merupakan polinom derajat n lebih besar dari 1, n merupakan elemen asli, bentuk rumus di atas dapat disederhanakan dengan skema di bawah ini dengan ketentuan tanda fungsi berselang-seling dari positif (+) menjadi (-) dan seterusnya.
| f(x) | g(x) |
| f’(x) | G1 |
| f”(x) | G2 |
| …. | …. |
| 0 | Gn |
Berdasarkan tabel di atas, bentuk integralnya dapat dituliskan sebagai berikut:
Agar lebih mudah dipahami, coba elo bahas soal di bawah ini.
Baca Juga: Aplikasi Integral: Cara Menghitung Volume Benda
Contoh Soal Integral Parsial
Pembahasan:
Pertama, buatlah permisalan. Ini akan lebih mudah jika terdapat pangkat 2 (polinom derajat 2). Elo bisa menggunakan skema untuk mengerjakan soal ini dengan lebih cepat.
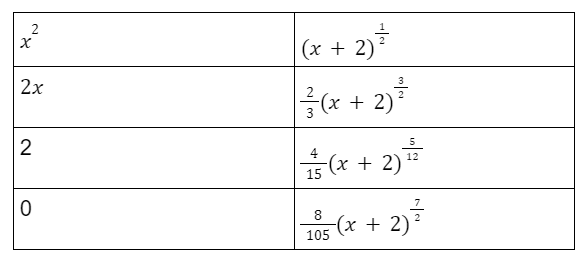
Sehingga, hasil dari persamaan di atas adalah:
Baca Juga: Integral Tentu: Konsep, Rumus, dan Contoh Soal
Pengertian Integral Substitusi
Jika integral ini menyelesaikan persamaan dengan permisalan, integral substitusi menyelesaikannya dengan mensubstitusi persamaan dalam bentuk yang lebih sederhana.
Rumus Integral Substitusi
Rumus integral substitusi dikenal dalam bentuk berikut:
Supaya elo lebih paham dengan persamaan ini, coba perhatikan contoh soalnya.
Baca Juga: Aplikasi Integral: Cara Menghitung Integral Luas
Contoh Soal Integral Substitusi
Pembahasan:
Jika u=x+3dx=du
Lalu, x=u-3
Lo dapat menemukan bahwa:
Nah, supaya elo bisa lebih paham lagi tentang integral parsial dan substitusi, elo bisa mempelajari materi dan membahas contoh soalnya di aplikasi Zenius, lho. Yuk, download aplikasinya atau klik banner di bawah ini untuk mempelajari materinya!
Referensi:
Video belajar Zenius. “Konsep Integral Susbstitusi”.
Kemdikbud. “Penerapan Integral dalam Kehidupan Masyarakat Sehari-hari”.
