Hai Sobat Zenius, di kesempatan kali ini gue mau ajak elo belajar tentang rumus permutasi dan kombinasi, sekalian intip perbedaan keduanya di artikel ini ya.
Nggak usah buru-buru ke rumus permutasi dan kombinasi ya. Dalam belajar materi permutasi dan kombinasi, gue pingin elo paham konteksnya dulu nih, perhatikan percakapan di bawah ini.
Coba elo bandingkan kedua percakapan di bawah ini.
Andi : “Gue minta tolong dong, cariin 3 orang buat masuk tim vokal gue!”
Dian : “Mau yang kayak gimana?”
Andi : “Bebas, yang penting suaranya oke.”
…dan,
Boy : “Lu, bagi nomor hp lo dong, gue mau ngirim tugas nih!”
Lulu : “Nih catet ya, 0897654321. Jangan salah ketik, nanti lo salah kirim deh.”
Boy : “Iya, tenang aja, makasih ya.”
Dari percakapan di atas, ada perbedaan yang mencolok di antara keduanya. Perbedaan tersebut terletak pada penggalan kalimat ini:
- “Cariin 3 orang buat masuk tim vokal gue”. Kita gak peduli tentang siapa aja atau urutan orangnya kayak gimana, yang penting ada 3 orang dan suaranya bagus.
- “Nih catet ya, 0897654321. Jangan salah ketik, nanti lo salah kirim deh”. Sekarang kita harus perhatikan urutannya. Kalau urutannya salah, maka nomor tersebut gak akan berfungsi atau bisa salah sambung, yang pasti itu bukan nomor Lulu. Jadi, harus sesuai urutan 0897654321.
Jelas ya perbedaannya, kalau poin pertama itu nggak peduli sama urutannya. Sedangkan, poin kedua sangat memperhatikan urutannya.
Nah, keduanya bisa disebut dengan kombinasi dan permutasi. Sebelum langsung ke rumus permutasi dan kombinasi, manakah yang termasuk kombinasi dan mana yang permutasi? Cari tau perbedaannya di bawah ini.
Perbedaan Kombinasi dan Permutasi
Dalam konsep peluang, dikenal juga istilah kombinasi dan permutasi. Keduanya digunakan untuk mencari peluang atau probabilitas dari suatu kejadian. Perbedaan yang mencolok dari keduanya, yaitu:
- Kombinasi (C) : cara menyusun objek tanpa memperhatikan urutan.
- Permutasi (P) : cara menyusun objek dengan memperhatikan urutan.
Contoh:
- Kombinasi
Suatu kelompok memiliki 3 orang anggota, yaitu A, B, dan C. Seorang guru harus memilih 2 orang anggota untuk mengikuti lomba vokal. Tentukan ada berapa kombinasi yang digunakan untuk mengambil dua orang dari tiga anggota yang tersedia!
Kombinasi adalah permutasi tanpa memperhatikan nilai acak. Karena pada kombinasi gak memperhatikan urutan, jadi cara yang bisa diambil dari kejadian di atas adalah A-B, A-C, dan B-C. Dengan begitu, ada 3 kombinasi cara untuk mengambil dua orang dari tiga anggota untuk menjadi peserta lomba vokal.
- Permutasi
Di dalam kotak, terdapat 3 buah bola yang masing-masing berwarna merah, kuning, dan hijau. Andi diminta untuk mengambil dua buah bola secara acak dan urutan pengambilannya harus diperhatikan. Tentukan ada berapa permutasi yang digunakan untuk mengambil dua buah bola dari dalam kotak tersebut!
Karena pada permutasi harus memperhatikan urutan, maka cara yang bisa diambil dari kejadian di atas adalah M-K, K-M, K-H, H-K, M-H, dan H-M. Jadi, ada 6 permutasi yang bisa digunakan untuk mengambil dua bola secara acak dan berurutan. Tentu rumus permutasi dan kombinasi nantinya akan berbeda.
Perbedaan permutasi dan kombinasi juga bisa elo lihat pada tabel berikut ini:
| Kombinasi | Permutasi |
| Urutan gak diperhatikan | Urutan harus diperhatikan |
| Memilih tim/kelompok, baju, mata pelajaran, daftar makanan | Menyusun orang, nomor telepon, angka, warna |
| Mengambil beberapa anggota dari grup | Mengambil ketua tim, menyusun jobdesk tiap orang |
| Mengambil dua warna dari kotak secara acak | Mengambil dua warna favorit dan berurutan |
| Mengambil tiga orang pemenang | Mengambil pemenang secara berurutan (juara 1, 2, dan 3) |
Udah jelas kan perbedaannya, oke sekarang kita lanjut ke pembahasan rumus permutasi dan kombinasi.
Rumus Permutasi
Udah tau perbedaan permutasi dan kombinasi kan? Nah, sekarang gue bakal kasih tau rumus permutasi dan kombinasi. Dimulai dari rumus permutasi dulu ya. Kenapa? Karena, permutasi punya beberapa rumus berdasarkan jenisnya. Langsung kita cek yuk!
Permutasi Unsur Berbeda (nPr)
Permutasi unsur berbeda ini maksudnya gimana ya? Elo udah lihat contoh kasus permutasi pada poin sebelumnya kan?
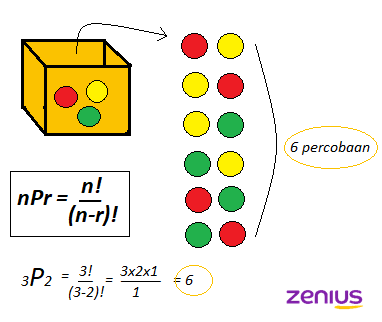
Yap, tentang bola di dalam kotak yang berwarna merah, kuning, hijau dan harus diambil 2 dari kotak secara acak dan berurutan. Sekarang kita pakai rumus nih ngerjainnya. Perhatikan gambar berikut ini:
Menggunakan perhitungan manual dengan mencocokkan warna hasilnya sama dengan rumus permutasi di atas, yaitu 6 percobaan.
Kenapa namanya permutasi unsur yang berbeda? Karena, dari total kejadian/objek yang bisa elo pilih, elo hanya disuruh mengambil sebagiannya, dan semua warna yang dipakai itu beda semua.
Kalau lihat contoh tadi ya berarti dari 3 bola, elo diminta untuk mengambil 2. Berarti ada 6 cara atau percobaan yang bisa elo gunakan untuk mengambil bola tersebut, bisa warna merah-kuning, hijau-merah, dll.
Jadi, untuk menghitung permutasi unsur yang berbeda, elo bisa menggunakan rumus permutasi seperti ini:
Keterangan:
P = permutasi
n = jumlah kejadian yang bisa dipilih
r = jumlah kejadian yang harus dipilih
! = simbol faktorial
Supaya lebih jelas, gue kasih contoh lainnya nih:
Ada anak Andi (A), Budi (B), dan Cecep (C) yang akan menempati 3 buah kursi di ruangan kelas. Tentukan variasi tempat duduk yang bisa dilakukan ketiga anak tersebut menggunakan konsep permutasi!
Penyelesaian:
Andi, Budi, Cecep → ABC, BCA, CAB, ACB, BAC, CBA = 6 variasi tempat duduk.
Kalau menggunakan rumus, berarti:
Udah makin jelas kan konsep tentang permutasi unsur yang berbeda? Intinya, permutasi unsur yang berbeda itu berarti semua unsurnya beda-beda.
Permutasi Unsur yang Sama
Meskipun konsepnya mirip-mirip namun rumus permutasi dan kombinasi berbeda, lho. Di dalam rumus permutasi terdapat berapa macam rumus? Nggak cuma satu dong
Selanjutnya, ada permutasi unsur yang sama. Gimana nih maksudnya? Apakah unsur-unsur penyusunnya ada yang sama?
Nah, untuk jenis permutasi yang satu ini, elo diharuskan untuk lebih teliti. Karena, elo tetap harus memperhatikan urutan tapi gak boleh ada unsur yang serupa atau diulang. Kita langsung masuk ke contoh deh biar gak bingung.
Ada susunan huruf A, B, dan A’. Tentukan variasi permutasi dari susunan huruf tersebut!
Penyelesaian:
ABA’ → AA’B, ABA’, A’BA, A’AB, BAA’, BA’A = 6 variasi tempat duduk (jika menggunakan konsep permutasi unsur yang berbeda).
Karena, sekarang yang diminta adalah permutasi unsur yang sama, sehingga gak boleh ada unsur yang serupa, jadi kita cek lagi ya:
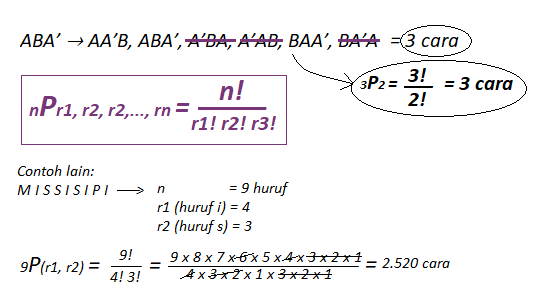
Permutasi Siklis
Selanjutnya, ada permutasi siklis atau melingkar. Maksudnya gimana? Permutasi ini digunakan untuk menentukan banyaknya cara penyusunan dari unsur yang berbeda dalam kondisi melingkar.
Contohnya, ketika ada perkumpulan yang duduknya melingkar, permainan melingkar (kucing dan tikus), posisi manik-manik pada gelang atau kalung, dll.

Nah, gimana sih cara atau variasi penyusunan orang yang berada pada lingkaran tersebut? Kita bisa menggunakan rumus permutasi siklis. Kita ambil contoh kayak kasus-kasus sebelumnya, yaitu menggunakan tokoh A B C.
Sekumpulan anak-anak akan duduk di meja bundar. Tentukan berapa variasi tempat duduk yang mungkin berdasarkan konsep permutasi!

Gampang banget kan, guys? Nah, rumus dari permutasi ini udah dibahas semua. Dari ketiga permutasi di atas, mana sih yang menurut elo paling mudah diingat?
Udah setengah jalan nih kita mempelajari rumus permutasi dan kombinasi. Lanjut terus yuk!
Rumus Kombinasi
Setelah membahas semua jenis permutasi, sekarang kita lanjut bahas rumus kombinasi yuk! Masih ingat kan bedanya kombinasi dengan permutasi?
Yap, kombinasi gak memperhitungkan urutan, sedangkan permutasi memperhatikan urutan. Nah disini nih yang membedakan rumus permutasi dan kombinasi. Berbeda dari permutasi, kombinasi hanya punya satu jenis aja.
Contoh kombinasi:
Ada 4 orang anak, yaitu Andi (A), Budi (B), Cecep (C), dan Dani (D). Guru meminta perwakilan 3 orang secara bebas untuk ikut lomba vokal mewakili sekolah. Tentukan berapa variasi tim yang terbentuk!
Penyelesaian:
Kita akan membentuk tim yang terdiri dari 3 orang saja tanpa memperhatikan urutannya, sehingga akan terbentuk variasi sebagai berikut.
A B C D → ABC, ABD, ACD, BCD = 4 variasi
Kalau mau diaplikasikan ke dalam rumus kombinasi adalah sebagai berikut.
Keterangan:
C = kombinasi
n = jumlah kejadian yang bisa dipilih
r = jumlah kejadian yang harus dipilih
! = simbol faktorial
Simple nya gini, rumus menentukan kombinasi dari n unsur diambil r unsur adalah
Kita kan sedang mempelajari rumus permutasi dan kombinasi. Kok belajar tentang rumus permutasinya lebih banyak, takut di bagian kombinasi malah bingung? Tenang aja kayak yang elo lihat sendiri, rumus kombinasi lebih sederhana kan.
Gue kasih satu pertanyaan lagi deh. Untuk nemu jawabannya elo perlu analisis nih, coba tulis jawabannya di komen ya.
Kombinasi yang benar dalam pernyataan berikut adalah ….
A. Terdapat 10 jenis menu makanan dan hanya 6 makanan yang bisa dipilih, maka kombinasinya adalah 220 variasi.
B. Dari 7 peserta hanya diambil 3 peserta terbaik kombinasinya adalah 35 variasi.
C. N unsur adalah 8 dan r unsur adalah 7, hasil kombinasinya adalah 65
Coba analisis satu-satu mana jawaban yang benar biar lebih paham rumus permutasi dan kombinasi.
Sejarah Permutasi dan Kombinasi
Udah belajar tentang rumus permutasi dan kombinasi .Tapi tau gak sih kapan tepatnya teori permutasi dan kombinasi ini muncul? Kita bahas secara singkatnya juga yuk!
Permutasi pada awalnya digunakan di China pada I Ching (Pinyin Yi Jing) sejak 1000 SM. Selanjutnya, Al Khalil (717-786) yang merupakan seorang matematikawan dan kriptografer asal Arab menulis Kitab Pesan Kriptografi yang berisi penggunaan permutasi dan kombinasi.
Selain itu, aturan permutasi juga udah ada dalam budaya India sejak tahun 1150-an oleh matematikawan India bernama Bhaskara II. Di tahun 1677, Fabian Stedman muncul dengan penjelasannya mengenai faktorial saat menjelaskan jumlah permutasi lonceng dalam perubahan dering.
Kemudian, ilmuwan asal Italia yang kemudian dinaturalisasi Perancis, Joseph Louis Lagrange pada tahun 1770 menemukan permasalahan yang membutuhkan bantuan permutasi.
Hingga akhirnya, Evariste Galois yang merupakan matematikawan asal Perancis dalam teori Galois memberikan deskripsi lengkap terkait apa yang mungkin dan gak mungkin dari persamaan polinomial. Hingga kini, dalam matematika modern, ada beberapa masalah yang memang harus diselesaikan dengan bantuan permutasi.
Sedangkan, untuk sejarah teori kombinasi ini diduga udah ada sejak 2800 SM. Sastra China memperkenalkan suatu kotak yang berisi susunan angka sedemikian rupa dengan baris, kolom, dan diagonalnya sama semua. Kombinasi dipakai untuk mempelajari kotak dan pola yang ada di dalamnya.
Nah, di abad ke-12, ada matematikawan asal India yang bernama Bhaskara Acharya dengan teori koefisien binomial, di mana teori ini sangat bergantung pada kombinasi.
Meskipun udah ada sejak lama, tapi ternyata kombinasi ini baru mendapatkan perhatian pada abad ke-17 oleh matematikawan Perancis bernama Blaise Pascal dan Pierre de Fermat.
Wah, setelah tau sejarahnya sungguh unik ya bahasan tentang rumus permutasi dan kombinasi ini.
Aplikasi Rumus Permutasi dan kombinasi dalam Kehidupan Sehari hari
Apa sih fungsi rumus permutasi dan kombinasi di dalam kehidupan kita sehari-hari? Banyak guys. Seperti menyusun telur dalam wadah dengan susunan yang berbeda, membuat plotingan pekerjaan saat kerja kelompok, membuat daftar piket, membuat susunan tempat duduk, memilih ketua kelas, memilih perwakilan kelas, memilih pakaian, dll.
Banyak juga kan aplikasi fungsi rumus permutasi dan kombinasi bagi kehidupan kita. Elo bisa menyebutkan contoh lain gak dari aplikasi kombinasi dan permutasi ini?
Oke, segitu dulu ya uraian tentang rumus permutasi dan kombinasi. Buat elo yang masih penasaran sama materi ini dan mau belajar tentang konsep lebih jauh lagi, Zenius udah menyediakan video pembelajaran yang bisa kamu akses secara gratis >> Rumus Permutasi dan Kombinasi.
Kalau elo ada pertanyaan tentang rumus permutasi dan kombinasi ini, langsung komen aja ya.
Elo juga bisa belajar materi seru lainnya dengan klik banner di bawah ini lalu tinggal ketik deh tuh elo mau belajar apa. Nanti elo bakal dapat penjelasannya dalam bentuk video sekaligus contoh soal serta pembahasannya.
Supaya proses belajar lo semakin efektif, Zenius punya beberapa paket belajar yang bisa lo pilih sesuai kebutuhan lo. Di sini lo nggak cuman mereview materi aja, tetapi juga ada latihan soal untuk mengukur pemahaman lo. Yuk klik banner di bawah ini untuk berlangganan!
Selamat belajar!
Baca Juga Artikel Lainnya
Rumus Peluang dan Aplikasinya dalam Kehidupan Sehari hari
Kumpulan Rumus Matematika Lengkap dengan Keterangannya
Poker: Permainan Menggunakan Teori Peluang
Originally published July 7, 2021
Updated by Silvia Dwi




thank you so much kak, membantu banget penjelasannya, make the math seems so simple and really fun 😉
Mudah banget dipahami, cara menjelaskannya mirip Bang Sabda ya, mantap😁👍