Halo Sobat Zenius! Apa kabar? Semoga sehat dan bahagia selalu ya! Kali ini gue mau ngajak elo belajar materi dinamika rotasi dan kesetimbangan benda tegar kelas 11.
Di artikel sebelumnya gue udah pernah membahas tentang dinamika partikel yang mana di dalamnya terdapat hukum-hukum Newton. Pasti elo udah baca dong?
Kalau belum, baca dulu ya agar elo bisa dengan mudah memahami pembahasan tentang dinamika rotasi ini.
Lho memang ada kaitannya ya? Tentu saja ada.
Materi dinamika rotasi dan kesetimbangan benda tegar ini erat kaitannya dengan Hukum II Newton. Jadi, untuk mempelajari ini ada baiknya elo memahami terlebih dahulu tentang dinamika partikel.
Okelah, dari pada berlama-lama, langsung aja kita bahas bersama-sama mengenai dinamika rotasi kelas 11 kurikulum 2013
Kesetimbangan Benda Tegar
Materi dinamika rotasi dan kesetimbangan benda tegar kelas 11 ini akan gue buka dengan pengertian dan konsep kesetimbangan nih.
Kesetimbangan benda tegar ini erat kaitannya dengan Hukum I Newton lho. Konsepnya menggunakan ΣF=0 dan Στ=0 (torsi).
Kesetimbangan adalah ketika suatu benda dianggap sebagai benda titik dengan ΣF=0, maka benda tersebut setimbang.
Namun, jika pada kesetimbangan benda tegar menggunakan syarat Στ=0.
Apa Itu Dinamika Rotasi?
Dinamika rotasi adalah ilmu yang mempelajari mengenai pergerakan benda yang berputar pada poros atau titik tumpunya.
Dinamika rotasi ini dipengaruhi oleh beberapa hal seperti massa, gaya, percepatan, kecepatan, torsi, dll. Dinamika rotasi ini sebenarnya menggunakan konsep Hukum II Newton, yaitu:
ΣF = m.a
Tetapi karena ia berotasi pada porosnya dan dipengaruhi oleh torsi, sehingga rumus dinamika rotasi menjadi:
Στ = I.α
Keterangan:
ΣF : resultan gaya (N)
m : massa/ukuran kelembaman (kg)
a : percepatan (m/s2)
Στ : momen torsi (Nm)
I : momen inersia (kgm2)
α : percepatan sudut (rad/s)
Ke depannya ketika elo mempelajari dinamika rotasi, maka elo akan menemukan rumus dengan bentuk baru dari gerak lurus atau translasi.
Jadi, elo tetap harus paham dulu mengenai gerak lurus yang mengikuti Hukum Newton.

Betul kan, dari gerak linear atau translasi itu rumusnya sama. Elo hanya tinggal menggantinya dengan lambang untuk dinamika rotasi.
Nah, kalo misalnya ada pertanyaan kayak gini: apa yang kamu ketahui tentang kesetimbangan dan gerak rotasi?
Kira-kira jawabannya apa?
Elo bisa menjabarkan dulu pengertian dari kesetimbangan dan gerak rotasi.
Kesetimbangan adalah adalah ketika suatu benda dianggap sebagai benda titik dengan ΣF=0. Artinya kesetimbangan adalah saat resultan benda bernilai 0 karena tidak ada gaya dan tidak ada torsi.
Sedangkan gerak rotasi gampangnya elo inget aja rotasi planet, jadi gerak rotasi adalah gerakan suatu benda terhadap sebuah titik pusat dan memiliki lintasan berbentuk lingkaran.
Nah, biar makin paham lagi, lanjut gue jelasin bagian yang lain dari materi dinamika rotasi dan kesetimbangan benda tegar kelas 11 ini ya, mulai dari momen gaya hingga soal dan pembahasan dinamika rotasi.
Akan tetapi, sebelum berlanjut ke pembahasan tersebut, Sobat Zenius baiknya download aplikasi Zenius dulu, nih!
Kenapa begitu? Sebab, lewat aplikasi elo jadi bisa makin produktif dalam belajar, nih! Di dalam aplikasi Zenius banyak sekali fitur menarik, seperti simulasi ujian try out, ribuan contoh soal dan pembahasan hingga mengasah otak lewat ZenCore bareng siswa lainnya.
Menarik, kan? Jadi, yuk, segera download aplikasi Zenius dengan klik banner di bawah ini!
Momen Gaya
Momen gaya atau torsi adalah suatu kecenderungan suatu gaya untuk memutar benda tegar terhadap titik poros tertentu.
Kalau bahasa simpelnya sih torsi ini merupakan suatu besaran yang dapat memutarkan benda. Lambang dari torsi adalah τ (tau).
Torsi ini pertama kali diperkenalkan ke dunia sains oleh seorang teknisi bernama J. Thomson, namun konsep torsi sebenarnya sudah ada jauh semenjak konsep tuas ditemukan oleh Archimedes. Kalau tuas, elo tentu udah mempelajarinya ya waktu SD, seperti jungkat-jungkit dan gunting kuku.
Gue ambil contoh sebuah pintu, ketika elo ingin membuka pintu, elo hanya perlu memutar engsel, dan tadaaa kemudian pintu terbuka.
Maka agar bisa bekerja, torsi dipengaruhi oleh engsel pintu sebagai titik tumpunya, gaya yang bekerja yaitu elo atau orang yang membuka pintu, dan lengan (jarak terhadap titik tumpu).
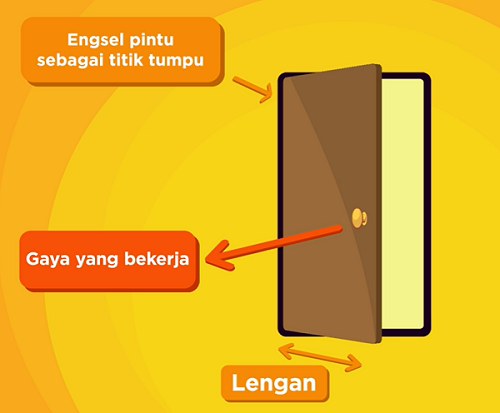
Nah, jadi besar kecilnya torsi dipengaruhi oleh poros/titik tumpu, gaya, dan jarak/lengan. Torsi merupakan perkalian antara gaya dan jarak. Kalau dituliskan rumus torsi akan menjadi seperti berikut ini:
τ = F.r
Keterangan:
τ : momen torsi (Nm)
F : gaya (N)
r : jarak gaya terhadap poros (m)
Oh iya, Torsi juga ternyata memiliki arah lho. Kalau arahnya berlawanan dengan jarum jam, berarti nilainya positif. Sedangkan, kalau searah jarum jam, maka bernilai negatif.
Torsi juga akan bekerja maksimal ketika gaya yang diberikan tegak lurus, yang berarti 90 derajat.
Tapi, kalau gayanya tidak tegak lurus itu bagaimana? Tentunya akan lebih sulit, rumusnya pun akan berbeda. Bisa dilihat pada ilustrasi berikut ini.
Dari ilustrasi di atas, maka rumus torsinya seperti ini:
τ = F.sin θ.r
Keterangan:
τ : momen torsi (Nm)
F : gaya (N)
r : jarak gaya terhadap poros (m)
θ : sudut antara r dan F (rad/s)
Momen Inersia
Sebelumnya kita udah tau nih kalau inersia adalah derajat kelembaman. Kalau inersia-nya besar, maka benda akan susah diputar.
Sebaliknya, kalau inersianya kecil, maka benda akan mudah untuk diputar. Inersia ini punya dua jenis lho, guys. Ada inersia benda titik atau partikel dan benda tegar.
Untuk momen inersia untuk benda titik bisa dirumuskan sebagai berikut:
I = m.R
Keterangan:
I : momen inersia (kgm2)
m : massa benda (kg)
R : jari-jari (m)
Sedangkan untuk momen inersia benda tegar, rumusnya disesuaikan tergantung dengan benda yang akan dihitung.
Benda tegar yang dimaksud itu seperti apa? Contohnya adalah silinder berongga, seperti jam dan batang. Elo bisa lihat rumus-rumusnya seperti ini:
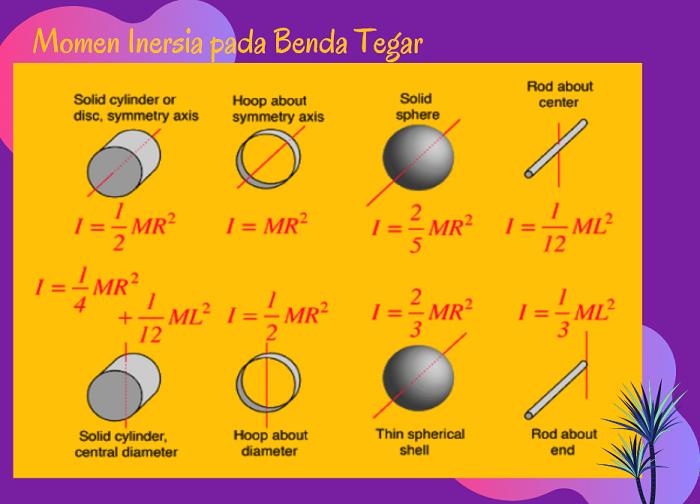
Nah, setelah elo mengetahui bentuk dari benda tegar yang akan dihitung momen inersianya, elo bisa langsung memasukkan rumusnya.
Momentum Sudut
Apa sih yang dimaksud dengan momentum sudut?
Momentum sudut atau L merupakan hasil perkalian antara momen inersia dengan kecepatan sudut benda.
Rumus momentum sudut adalah sebagai berikut:
L = I ω
Keterangan:
L : momentum sudut (kgm²/s)
I : momen inersia (kgm²)
ω : kecepatan sudut benda (rad/s)
Energi Kinetik Dinamika Rotasi
Energi kinetik ada dua bagian lho, guys. Ada energi kinetik translasi dan rotasi.
Gerak Translasi
Gerak translasi adalah suatu gerak yang arahnya lurus atau melengkung. Gerak ini udah sering kita pelajari sebelumnya. Jadi, pastinya udah gak bingung lagi ‘kan?
Contohnya pada gerak translasi itu apa sih? Misalnya ada balok dengan massa M ditarik ke kanan dengan kecepatan V.
Maka, rumus energi kinetik gerak translasi adalah sebagai berikut:
Ek = ½ m.v²
Keterangan:
Ek : energi kinetik (joule)
m : massa benda (kg)
v : kecepatan (m/s)
Gerak Rotasi
Gerak rotasi adalah suatu gerak yang arahnya mengalami perputaran terhadap poros tertentu. Nah, gerak ini dipengaruhi oleh torsi. Sebelumnya kita udah belajar juga tentang torsi.
Contohnya gerak rotasi itu apa? Contohnya adalah bola yang berputar pada porosnya. Maka, rumus energi kinetik gerak rotasi adalah sebagai berikut:
Ek = ½ I.ω²
Keterangan:
Ek : energi kinetik (joule)
I : momen inersia (kgm²)
ω : kecepatan sudut (rad/s)
Contoh Soal Dinamika Rotasi dan Kesetimbangan Benda Tegar
Supaya elo makin paham dengan materi yang satu ini, gue udah menyiapkan beberapa contoh soal dan pembahasan dinamika rotasi dan kesetimbangan benda tegar. Langsung cek aja di bawah ini ya:
Contoh Soal 1
Pada katrol berupa silinder pejal dililitkan tali dan ditarik dengan gaya sebesar 40 N. Massa katrol tersebut adalah 2 Kg dengan jari-jari 0,5 m. Akibat gaya tersebut, berapa percepatan sudut dan percepatan tangensial yang dialami oleh katrol?
Pembahasan 1
Inersia untuk silinder pejal menggunakan rumus : I = ½mR².
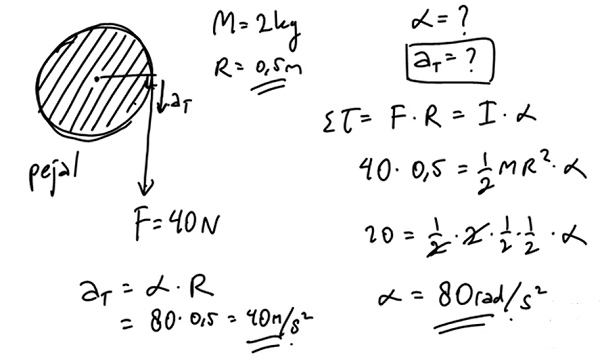
Contoh Soal 2
Sebuah bola pejal memiliki massa sebesar 10 kg. Jari-jari yang dimiliki oleh bola pejal tersebut adalah 1 m.
Bola tersebut berputar pada porosnya dengan kecepatan sudut sebesar π rad/s. Tentukan energi kinetik dari bola pejal tersebut!
Pembahasan 2
Inersia untuk bola pejal menggunakan rumus: I = 2/5 mR².
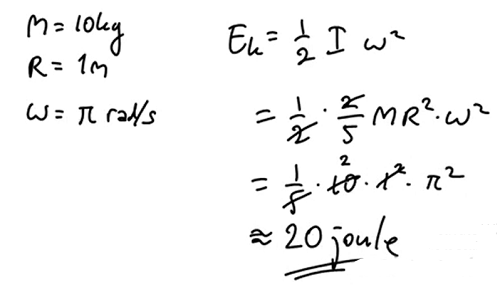
Belajar konsep udah, latihan soal juga udah. Berarti udah paham dong sama materi dinamika rotasi dan kesetimbangan benda tegar kelas 11 ini?
Kalau elo tertarik buat belajar materi yang satu ini lewat video pembelajaran, elo juga bisa, kok, belajar dari Zenius!
Video pembelajaran Zenius dibawakan oleh tutor-tutor yang terpercaya sehingga materi dijamin akan dikemas dengan menarik dan mudah dimengerti! Nggak cuman itu, tutor juga akan memberikan beberapa contoh soal dan pembahasan yang bisa membuat elo makin ngerti tentang materinya
Buat aksesnya, elo tinggal klik banner di bawah ini, ya!
Terus, kalau elo mau semakin matang dalam menghadapi ujian sekolah, Zenius punya beberapa paket belajar yang menarik buat, elo! Langsung aja klik banner ini ya!

Baca Juga Artikel Materi Fisika Lainnya
Dinamika Partikel dan Hukum Newton
Originally Published: January 14, 2021
Update by: Sabrina Mulia Rhamadanty & Maulana Adieb






Maaf Kak, sepertinya momen inersia pada silinder pejal itu 1/2 mR² tetapi pada pembahasan 1 ditulis I = mR2. Terima kasih Kak sebelumnya..
wah iya salah ketik, terima kasih ya udah ngoreksi, kamu teliti banget 😀 tapi, untuk pembahasan contoh soal dan rumus di gambar udah betul yaa pakai 1/2 mR².
Itukan udah 1/2 mr2