Ada yang masih bingung ngerjain contoh soal logika proposisi/kuantor TPS/TPA yang ada kata “jika-maka” atau “semua-ada”? Nah, ini adalah jenis soal TPS/TPA Logika proposisi.
Pas banget nih, di artikel kali ini gue akan membahas tuntas tipe soal dan contoh soal logika proposisi supaya elo siap menghadapi UTBK SBMPTN.
Bisa dibilang jenis soal yang memiliki nama lain Logika Kuantor ini adalah jenis soal yang gak pernah absen muncul di SBMPTN.
Tapi kalo elo masih bingung ngerjain jenis soal ini, jangan khawatir karena gue udah nyiapin contoh soal logika proposisi lengkap dengan jawabannya yang bisa langsung elo cek di bawah ini.
Tipe Soal TPS/TPA Logika Preposisi/Kuantor
Sebelum elo masuk ke contoh soal logika proposisi, elo wajib kenalan dulu dengan tipe-tipe soal yang sering keluar dalam SBMPTN.
Setidaknya ada tiga jenis tipe soal logika kuantor yang sering muncul. Yang pertama adalah soal hubungan “jika, maka”, yang kedua “dan, atau” dan yang ketiga “semua ada, beberapa dan sebagian”.
Nah, supaya lebih jelas, elo bisa langsung cek penjelasan masing-masing jenis logika kuantor di bawah ini:
(1) Contoh Soal Logika Proposisi “Jika-Maka”
Soal di atas diambil dari SBMPTN 2013. Klik di sini untuk mengakses selengkapnya.
(2) Contoh Soal Logika Proposisi “Dan & Atau”
Soal di atas diambil dari SBMPTN 2009. Klik di sini untuk mengakses selengkapnya.
(3) Contoh Soal Logika Proposisi “Semua-Ada, Beberapa, dan Sebagian”
Soal di atas diambil dari SNMPTN 2009. Klik di sini untuk mengakses selengkapnya.
Untuk soal logika proposisi tipe “jika-maka” dan “dan & atau”, biasanya jarang ada salah alias pembuat soal sudah udah mengikuti aturan logika dengan benar.
Tapi elo perlu memberikan perhatian ekstra di tipe soal ketiga alias tipe soal logika proposisi “semua-ada, beberapa, sebagian”.
Karena dalam beberapa soal SBMPTN masih mengalami banyak kesalahan soal. Nah, supaya menghindari elo dari kebingungan kalo tipe soal yang satu ini muncul, elo harus bisa mengetahui kemauan si pembuat soal.
Ada dua jenis dasar logika yang biasanya digunakan dalam menggunakan rumus penalaran logis sebelum membuat soal yaitu logika yang tertutup dan terbuka.
Waduh, apaan tuh?
Sini gue jelasin.
Dasar Berpikir Logika TERTUTUP
Artinya, elo NGGAK BOLEH masukin data lain selain dari premis yang dikasih.
Jadi, elo harus menarik kesimpulan HANYA dari premis yang tersedia aja, dan nggak boleh ada asumsi atau tambahan apa pun.
Dasar Berpikir Logika TERBUKA
Artinya, elo boleh nih masukin info-info tambahan lain yang kita tau (yang gak ada di premis).
Jadi, dalam menarik kesimpulan, cenderung lebih bebas, gak terpaku dengan premis yang dikasih.
Pada tipe soal SBMPTN yang “jika-maka”, “dan & atau”, umumnya elo diharuskan berpikir dengan logika tertutup.
Tapi di soal tipe “semua-ada” ini yang suka ambigu dan gak jelas pilihan jawabannya.
Jadi, yang akan gue ajarin di sini adalah cara ngejawab soal tipe “semua-ada” dengan cara tertutup (menarik kesimpulan cuma dari premis yang dikasih).
Nah, supaya makin paham, gue langsung kasih aja contoh soal logika proposisi tipe “semua-ada” lengkap dengan pembahasannya ya.
1. Bentuk SEMUA (All) Simbol: ∀
Contoh premis:
“Semua semut adalah serangga”
Dalam logika modern yang benar, cara memperlakukan bentuk “semua” adalah sama dengan “jika… , maka…”. Jadi untuk premis “Semua semut adalah serangga” artinya sama dengan:
“Jika ada semut, maka dia adalah serangga.” (jika p, maka q).”
-> Kita bisa menganggap p = semut, q = serangga.
Ini wajib diinget sepenuh hati.
Nah, biasanya gue menyebut bentuk ini adalah bentuk SYARAT.
Premis “Jika ada semut, maka dia adalah serangga” itu kan artinya KALAU (IF) ada sesuatu yang berupa semut, maka dia adalah serangga.
Jadi, elo baru suatu keadaan di mana jika p terjadi, maka q pasti akan terjadi. (Masih KALAU loh ya, belum ada yang bilang kalo udah terjadi).
Jadi, kalo gue tanya, “Himpunan semut di sini udah pasti ADA belom?“
Jawabannya adalah belum tentu; karena ini masih berupa SYARAT dan belom ada premis yang bilang kalo udah terjadi.
Nah, mungkin ada yang masih bingung, tapi nggak papa, kita lanjut aja dulu.
2. Bentuk TIDAK ADA (No)
Contoh premis:
“Tidak ada pemain bola yang suka makan coklat.”
Ini cara memperlakukannya mirip sih dengan yang bentuk “semua” tadi. Kalo mau diubah ke bentuk SYARAT, bahasanya jadi:
“Jika ada pemain bola, maka dia tidak suka makan coklat.”
Maknanya sama aja dengan premis tadi: “Tidak ada pemain bola yang suka makan coklat”. Okee?! Sip. Kita lanjut..
3. Bentuk ADA (Some) Simbol: ∃
Contoh premis:
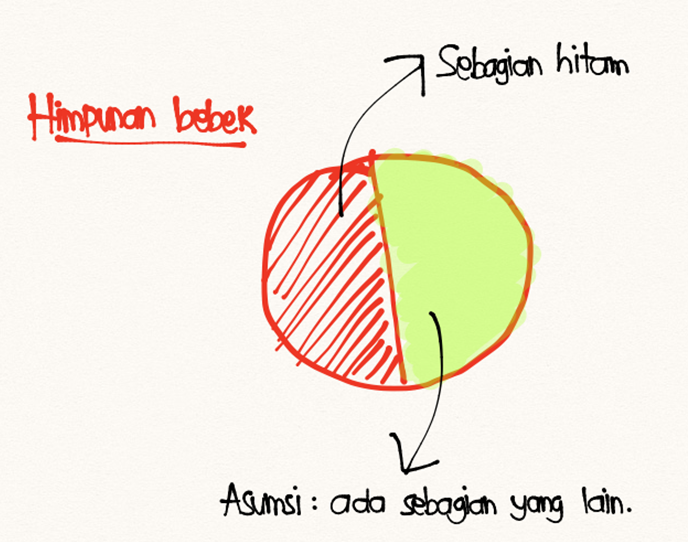
- a) Ada bebek yang berwarna hitam.
- b) Beberapa bebek berwarna hitam.
- c) Sebagian bebek berwarna hitam.
Di soal TPA, elo bakal sering ketemu dengan bentuk b) dan c) yang menggunakan kata “beberapa” dan “sebagian”. Sayangnya, bentuk yang ini adalah bentuk yang salah.
Di aturan logika yang benar, bentuk ini asalnya adalah dari kata “some” yang artinya SELALU “at least one”.
BUKAN: “a few”, “many”, “lots”, “at least a few”, “at least one but not all”, “at least one and maybe all”, “at least a few but not all”.
Jadi, terjemahan bahasa Indonesianya yang tepat adalah “Ada” (paling tidak, satu).
“Ada” di sini menunjukkan bahwa sesuatu itu benar-benar exists.
Jadi, untuk premis “Ada bebek yang berwarna hitam” artinya: paling tidak, ada satu bebek yang berwarna hitam. Bandingkan dengan:
“Beberapa bebek berwarna hitam” atau “Sebagian bebek berwarna hitam”
Kalo menggunakan “beberapa” dan “sebagian”, akan bisa muncul suatu asumsi bahwa akan ada sebagian lagi yang warnanya bukan hitam/putih/lainnya. Ya kan?
Di mana itu menyalahi aturan logika awal, walaupun misalnya di keadaan sebenarnya emang ada bebek yang warnanya nggak item.
Tapi, kalo elo mau narik kesimpulan cuma berdasarkan premis yang dikasih, asumsi “sebagian bebek berwarna tidak hitam” jadi salah.
Okee. Bisa dimengerti? Jadi, yang penting adalah, elo harus selalu inget:
Nah, itu adalah pengertian dasarnya. Sekarang, gimana caranya kalo ada dua premis dan kita disuruh untuk nentuin mana kesimpulan yang valid? Bisa pake dua cara nih buat ngerjainnya.
Pertama, pake penalaran dengan pengertian dasar yang tadi. Kedua, bisa pake visualisasi Diagram Venn.
Gue bakal jelasin dua-duanya. Nah, elo bisa milih cara manapun yang elo suka. Okee. Kita mulai ya.
Contoh Soal Logika Proposisi – Dua Premis
Contoh Soal 1
Coba perhatikan contoh soal logika proposisi dengan dua premis berikut ini:
Premis:
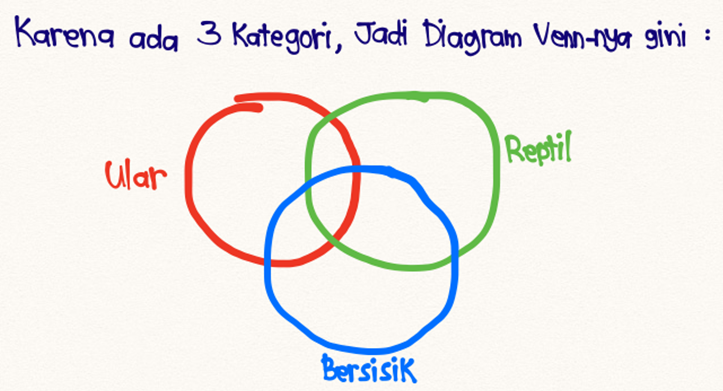
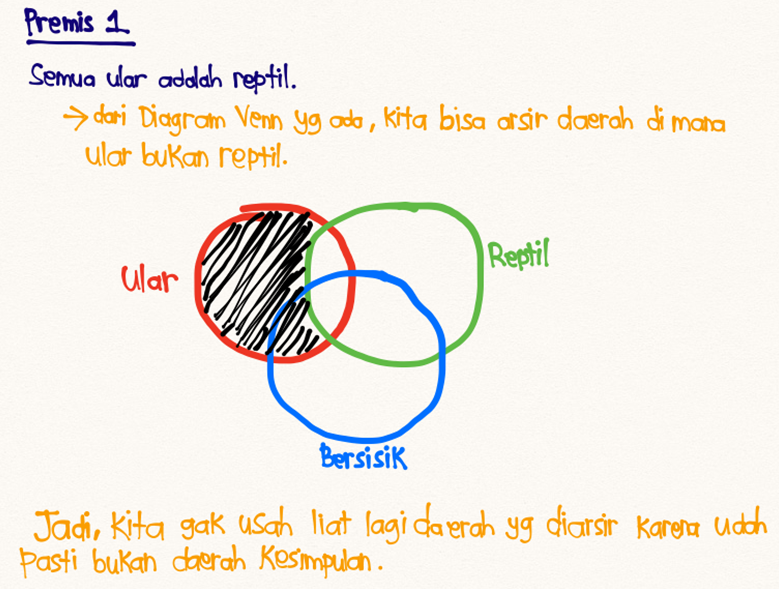
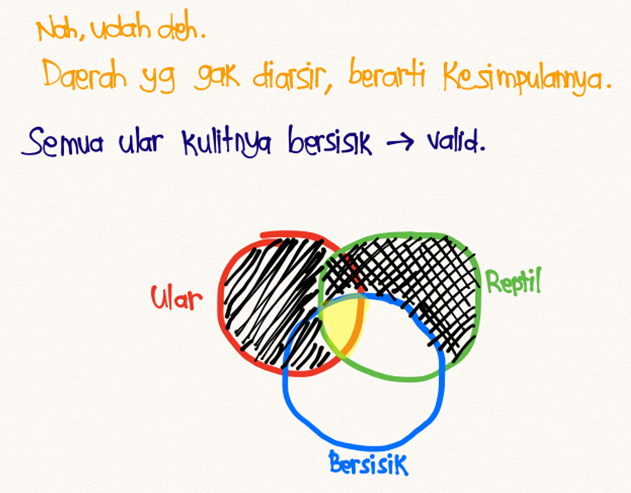
- (1) Semua ular adalah reptil
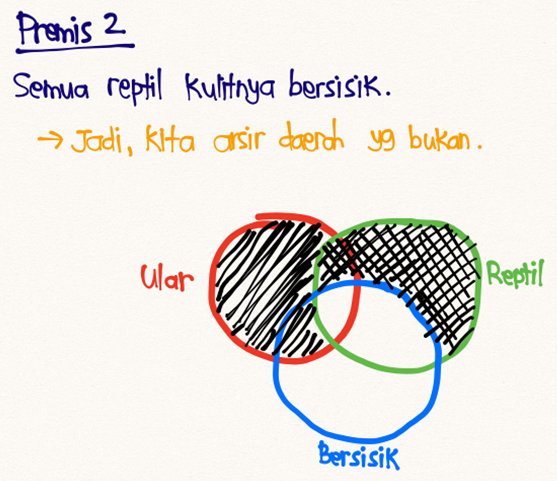
- (2) Semua reptil kulitnya bersisik.
Kesimpulan : Jadi, semua ular kulitnya bersisik.
Pertanyaan : Kesimpulannya valid/ invalid?
Jawab:
Kalo mau pake cara biasa, kita bisa ubah bentuk premis (1) dan (2) jadi bentuk SYARAT, ya kan, karena memang bentuk “semua” sama dengan “jika-maka”
- (1) Jika ada ular, maka dia adalah reptil.
- (2) Jika ada reptil, maka kulitnya bersisik.
Kita bikin aja p = ular, q = reptil, r = bersisik
(hurufnya gak mesti gini juga sih, bebas-bebas aja, asal bisa ngerti tulisan elo sendiri)
Jadi bentuk premisnya:
- (1) p ->q
- (2) q ->r
Kesimpulan yang ada di soal: Jika ada ular, maka kulitnya bersisik (p ->r). Nah, jadi kesimpulannya VALID. Kalo mau pake visualisasi Diagram Venn juga boleh.
Contoh Soal 2
Coba perhatikan contoh soal logika proposisi dengan dua premis berikut ini:
Premis:
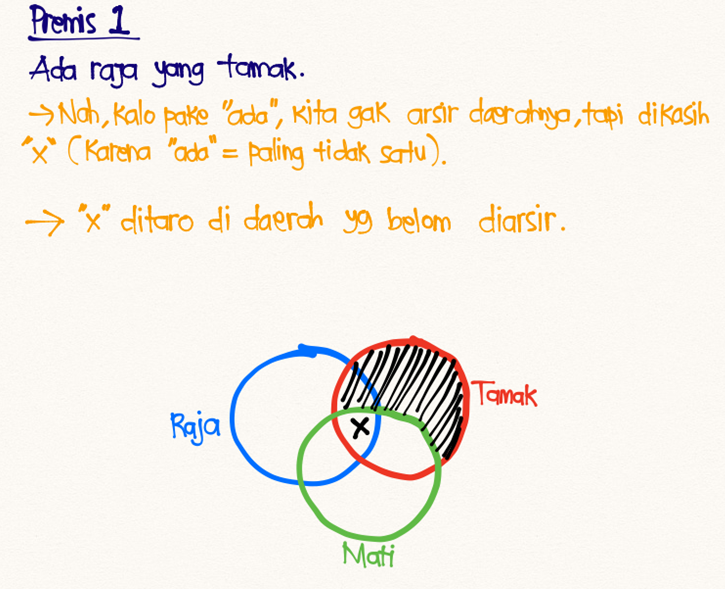
- (1) Ada raja yang tamak
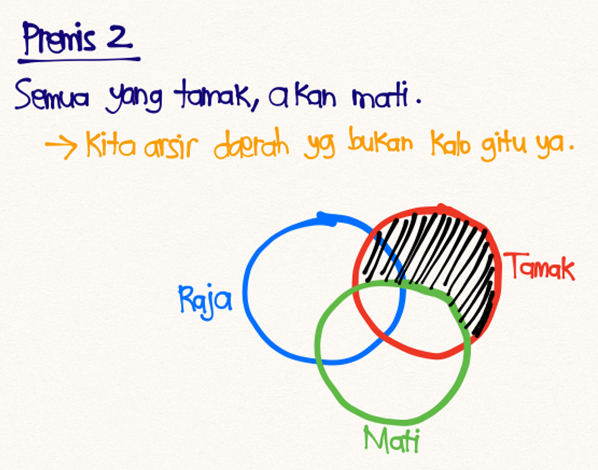
- (2) Semua yang tamak, akan mati
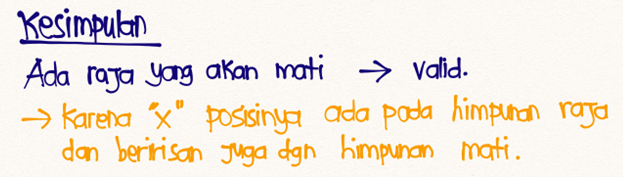
Kesimpulan: Jadi, ada raja yang akan mati.
Pertanyaan: Kesimpulannya valid/ invalid?
Jawab:
Penjelasan pake cara penalaran dasar biasa:
Kalo kita liat premis (1): “Ada raja yang tamak” akan sama artinya dengan “Ada yang tamak, yang dia adalah raja” (dibolak-balik sama aja, tapi inget, KHUSUS yang bentuk “ADA”).
Dari premis (1), kita bisa liat bahwa himpunan “yang tamak” itu ADA, “raja” juga ADA.
Nah, premis (2) kan bentuknya “semua” tuh, sama kayak bentuk SYARAT kan.
Jadi, kita bisa bilang: “Jika ada yang tamak, maka dia akan mati”.
Ya udah deh, kalo syaratnya gitu, jadi yang tamak pasti bakal mati kan, di mana yang tamak itu adalah rajanya.
Jadi udah pasti kesimpulannya: “ADA raja yang akan mati”. Kesimpulan VALID.
Nah, cara kedua, pake diagram Venn:
Contoh Soal 3
Premis:
- (1) Semua orang adalah kucing
- (2) Beruang bukan kucing
Apa kesimpulan dari kedua premis di atas?
Kalo mau pake cara biasa, elo bisa ubah bentuk premis (1) jadi bentuk SYARAT, ya kan, karena memang bentuk “semua” sama dengan “jika-maka”
- (1) Jika ada orang, maka dia adalah kucing.
Kita bikin aja p = orang, q = kucing.
Nah, bentuk premis ke (2) gak bisa jadi bentuk syarat karena udah mutlak bahwa beruang bukanlah kucing.
- (2) Beruang bukan kucing.
Kita bikin aja p = orang, q = kucing, r= beruang:
Jadi bentuk premisnya:
- (1) p = q
- (2) q ≠ r
Kesimpulan yang ada di soal artinya (p ≠ r). Nah, jadi kesimpulannya beruang bukanlah orang.
Nah, itu tadi ada tiga contoh soal dan cara jawabnya. Sebenernya masih ada banyak kombinasi soal, tapi segini dulu ya.
Nah, itu tadi ada dua contoh soal dan cara jawabnya. Sebenernya masih ada banyak kombinasi soal, tapi segini dulu ya.
Kumpulan Latihan Soal SBMPTN TPS & TPA Logika Proposisi
Kalo elo mau latihan soal yang mirip kayak dua soal di atas, bisa cobain interactive module yang berisi contoh soal logika proposisi di link Zenius Education berikut ini:
Zenius.net juga menyediakan soal dan video pembahasan TPS / TPA Logika Proposisi dari SBMPTN tahun-tahun lalu. Silakan dilahap:
- Soal + Pembahasan SBMPTN TPS / TPA Logika Proposisi 2018
- Soal + Pembahasan SBMPTN TPS / TPA Logika Proposisi 2017
- Soal + Pembahasan SBMPTN TPS / TPA Logika Proposisi 2016
- Soal + Pembahasan SBMPTN TPA Logika Proposisi 2015
- Logika proposisi ga keluar di SBMPTN 2014
- Soal + Pembahasan SBMPTN TPA Logika Proposisi 2013
- Soal + Pembahasan SBMPTN TPA Logika Proposisi 2012
Elo bisa download soal-soal di atas dalam bentuk pdf GRATIS! dan tersedia juga video pembahasannya.
Dan bukan cuma soal TPS/TPA aja, Zenius juga udah punya ribuan paket soal lengkap yang bisa elo download secara GRATIS.
Soal-soal ini dibuat sama tutor Zenius dengan referensi yang berkualitas. Setiap soalnya juga sudah pasti mengandung soal HOTS. Kalau elo mau download soalnya, elo bisa download aja di zenius.net!
Okey… Mudah-mudahan bisa dimengerti ya. Selamat belajar dan see you later!
Dan kalo ada di antara elo yang mau ngobrol atau diskusi sama Wilona tentang persiapan SBMPTN TPA, khususnya materi dan contoh soal logika proposisi, langsung aja tinggalin comment di bawah artikel ini.
Atau buat elo yang masih bingung gimana caranya belajar SBMPTN yang efektif, gua sangat menyarankan untuk belajar melalui Zenius yang udah kita update dengan bahan materi SBMPTN yang paling lengkap sebagai senjata utama elo menghadapi SBMPTN.
Di website Zenius Education, elo bisa mendapatkan akses ke-66.000 video pembahasan materi dan 3.000 paket latihan soal, termasuk pembahasan soal UN, SBMPTN, dan Ujian Mandiri dari beberapa perguruan tinggi ternama, seperti SIMAK UI, UTUL UGM, USM STAN. Biar persiapan elo menuju kampus impian makin mantap, elo juga bisa ikutan Zenius Ultima Plus. Caranya cukup klik banner di bawah ini!
Originally Published: April 4, 2018
Update by: Sabrina Mulia Rhamadanty








wahhh super sekali kak wilona! (y)
tapi saya juga mau nanya banget nih ka, tentang jawab soal logika, soalnya saya senang banget latihan TPA, tapi sayangnya, ka wilona tuh untuk jawab soal logika di snmptn/sbmptn gak pernah pake diagram venn.. jadi saya kurang terlatih ka untuk jawab soal logika memakai diagram venn.. sedangkan di buku latihan TPA yang saya liat kebanyakkan memakai diagram venn.. saya gak beli soalnya susah belajar pake buku.. saya minta tolong dong ka, kalau bisa sih bikin konten latihan TPA lagi yang 2013 kan ada 4 paket tuh soal SBMPTNnya untuk logika jelasin pake diagram venn.. hehe ^^V makasih ka, nice post!
nah ini kak, baru mau komen gini hehehe
oke siip 😀 jawabannya di atas brarti ya.
kak secepatnya yaa.. kalo bisa sebelum un lah biar lebih banyak latihannya
iya. hehe emg yang di zeniusnet belom ada, dan materi yg gw tulis ini bakal gw bikin videonya kok. 🙂 nanti bakal ada juga contoh2 yang pake diagram venn. ditunggu yaa. mudah2an bisa direkam cepet.
sebenernya kmrn2 blm ada soalnya gw agak kurang suka diagram venn, kalo keseringan make diagram venn lama2 jadi mekanis gt ngerjainnya. udh otomatis bs nemu jawabannya tampa mikir. pdhl yang penting justru mikirnya. tapi ternyata masih banyak yang kesusahan kalo gak pake visualisasi, jd gw br berencana ngerekam thn ini deh.
thanks masukannya yaaa.. 😀
makasih ka Wilona, sangat bermanfaat.
tapi boleh ga ka lebih dipaparin lagi jenis-jenis silogisme. menurut buku yang pernah kubaca, soal SBMPTN itu menggunakan banyak jenis silogisme, seperti SILOGISME HIPOTESIS BENTUK KHUSUS. thank’s kaka. 🙂
iyaa ini contoh silogismenya emg baru 2, di buku yg gw pake juga ada banyak kombinasinya. rencanya mau gw bikin jadi video aja d zeniusnet krn kalo ditulis kepanjangan banget. hehe.
nah tapi gw gak begitu afal nama2 pastinya, kalo silogisme hipotesis bentuk khusus itu yg contohnya gimana? thanks masukannya yaa 😀
kak aku gak ngerti soal yg analitik.yg ada banyak informasinya, trus kita disuruh nyusun misalnya dari yg menang sampe yg kalah begitu kak gmn?
nah, udah pernah liat pembahasan soal di zenius.net? ada beberapa soal analitik dari snmptn + pembahasannya. coba klik di sini deh
https://www.zenius.net/lp/cg191/kumpulan-soal-snmptn
(1) Semua ular adalah reptil
(2) Semua reptil kulitnya bersisik.
kalau gw mikirnya reptil itu himpunannya belum tentu cuma ular itu berarti gw pake cara berpikir “TERBUKA” yaa..
wah selama ini gw salah berarti waktu snmptn
makanya dibetulin mas 😀
permisi, nanya dong kak,
soal ini jawabannya apa ya kak?
semua pesawat terbang memiliki roda,
sebagian pesawat terbang bemesin ganda.
simpulan yg tepat adalah?
a. semua pesawat terbang yg bermesin ganda dan memiliki roda.
b. semua pesawat terbang bermesin tunggal dan memiliki roda.
c. sebagian pesawat terbang bermesin ganda dan tidak memiliki roda.
d. sebagian pesawat terbang tidak bermesin ganda dan memiliki roda
e. semua pesawat terbang yg memiliki roda dan bermesin ganda.
makasi:)
jawabannya D :))
jawabn D lebih mendingan. cuman menurut gua pernyataan “sebagian(atau bisa kita ganti “ADA”) Ada pesawat terbang tidak bermesin ganda dan memiliki roda
“Ada pesawat terbang tidak bermesin ganda” kalo di perhatiin kayak nya agak aneh menurut gua soal nya liat dr premis 2(sebagian pesawat terbang bemesin ganda) kan maksud nya ADA loh pesawat terbang bermesin ganda
nah “apakah ada pesawat terbang tidak bermesin ganda?” jawaban gua sih GATAU karena gaada pernyataan yg menyatakan itu.
atas gue bener nih jawabannya, hehe klo ngikutin pembuat soal ya jawaban yg mendingan yg D, tapi klo diliat dari premis yg ada, kita gak bisa menyimpulkan sebagian pesawat terbang tidak bermesin ganda
Ka, di SBMPTN 2013 yang No. 10 => “Master:… ~ Dewasa:…” // bukankah jawabannya Doktor – Tua? analoginya kan, (Master) satu tingkat jadi (Doktor) dan (Dewasa) satu tingkat jadi (Tua)
suara kk wilona ini bkin mkin smngat bljar aj..haha
Waaaah terima kasih atas tipsnya kakak 😀 do’ain yah semoga lulus di sbmptn 2014 ini 🙂
Gue kok kalo pake diagram venn malah jadi bingung sendiri ya O_O
kak kalo semua ular adalah reptil tuh gambar diagram vennnya bukannya lingkaran dalam lingkaran kan ka? jadi lingkaran ular d dlm lingkaran reptil??
itu namanye malpractice in education, yang benar diagram venn nya: lingkaran dalam lingkaran.
ka cara ngerjain soal diagram venn dong
waah mbak wilona mantep banget infonya, makasih 😀
Detail dan mudah dimengerti ? nice post …
Kak. Kok banyak banget pembahasan sbmptn logika yg kk anggap salah?? Apa tutor udh konsultasi ke dosen yg ahli dalam logika ? Jawab plis, biar keraguan ini tidak menghantui kuh :b
Dear, Mbak Wilona!
Saya perhatiin penjelasan penjelasan tentang penarikan kesimpulan koq sedikit berbeda dengan pemahaman saya, mohon bantuan untuk mencari bahan rujukan dari materi tersebut. Setahu saya kalau penarikan kesimpulan dengan Deduksi tuh ada dengan Modus Ponens, Modus tollens, Silogisme Hipotetis dan Silogisme Kategorik, Silogisme Disjungsi, Silogisme alternatif, Dilema, Simplikasi, dll. Kalau dari penjelasan diatas koq menyamakan materi Silogisme Kategoris dan Hipotetis? saya melihat ada kerancuan. Saya ada buku lokal yang pernah saya baca. “Maaf saya tidak punya teks bahasa Inggris”
1. Pengantar Logika karangan Rafael Raga Maran penerbit Grasindo,
2. Pengantar Logika-asas-asas penalaran sistematis tulisan Jan Hendrik Rapar terbitan Kanisius.
3. Logika karangan Drs.H.Mundiri terbitan RajaGrafindo Persada”
Dari beberapa buku tersebut, ada aturan baku diantaranya adalah silogime kategori dan silogisme hipotetis dan sepengetahuan saya itu memiliki cara dan aturan yang berbeda.
Terimakasih!
Kenny, pemain bulutangkis klub Jaya, dapat melakukan service forehand dengan baik Setiap pemain yang bisa melakukan service forehand yang baik dapat melakukan drop shot akurat (A) Beberapa pemain bulutangkis klub Jaya dapat melakukan dropshot yang akurat (B) Semua pemain bulutangkis klub Jaya dapat melakukan service forehand dengan baik dan dropshot yang akurat (C) Beberapa pemain bulutangkis klub Jaya dapat melakukan service forehand dengan baik dan dropshot yang akurat (D) Beberapa pemain bulutangkis klub Jaya tidak dapat melakukan service forehand dengan baik tetapi bisa melakukan dropshot yang akurat (E) Semua pemain bulutangkis dapat melakukan service forehand dengan baik dan dropshot yang akurat
Kalo aku ngisi soal gini dicoret yg tengahnya, misalnya ada raja yg tamak – semua yg tamak akan mati, nah tamaknya dicoret jadi “ada raja yg akan mati”. diagram venn malah bingung
Mksh ya kakak, bermanfaat sekali
terima kasih kak untuk share materinya, tetapi saya masih bingung dengan penjelasan dengan menggunakan diagram venn. Padahal dari daerah yang tidak diarsir masih ada “ular”, “reptil”, dan “bersisik”. Apalagi untuk soal yang menggunakan “semua” dan “ada”. Saya lebih paham jika dalam penarikan kesimpulan bentuk “semua A adalah B” diubah menjadi “jika A, maka B” daripada menggunakan diagram venn. Tetapi untuk contoh nomor 2 tidak diberi contoh untuk bentuk yang “jika… maka …” sehingga cukup sulit untuk menyimpulkan. Mohon pencerahannya kak.
Sangat membantu kak! Saya jadi ngk harus berpikir terlalu keras dalam mengerjakan soal TPA.
kak willona bs ngak kita blajarx di bab 5 logika kls 10 trus lanjut ke SBMPTN deductive
Wah..saya sebagai pembaca mengerti sekali dengan bahasa yang Anda gunakan Terimakasih..